Volume 16, No. 4 (Winter 2013)
ABSTRACT: The purpose of this paper is to explain the marginal efficiency of capital.1 The net present value diagram is derived and used to illustrate how the interest rate regulates the intertemporal allocation of resources. The net present value diagram is then used to show that the marginal efficiency of capital contradicts the net present value method of ranking investment projects. The net present value diagram is integrated into the capital-based framework to demonstrate that the interest rate cannot regulate the intertemporal allocation of resources in Keynes’s theory of investment.
KEYWORDS: John Maynard Keynes, marginal efficiency of capital, net present value, economic calculation, interest rates, interest rate sensitivity, intertemporal allocation of resources, central banking, business cycles, capital-based macroeconomics
JEL CLASSIFICATION: E12, G30, E22, E32, E43, E52, 58
INTRODUCTION
Economic calculation plays a central role in Austrian economics and Keynesian economics. However, the Austrians and the Keynesians each advocate a different approach to economic calculation. The Austrian school advances the present value approach to economic calculation in which the net present value is used to rank investment projects. In distinct contrast, the Keynesians adopt the rate of return approach to economic calculation in which the marginal efficiency of capital is used to rank investment projects. The purpose of this paper is to explain the marginal efficiency of capital and its implications for macroeconomics.2
NET PRESENT VALUE
Ludwig von Mises and Irving Fisher advocate the present value approach to economic calculation. According to the present value approach, the price of an investment project tends to equal the present value of the project’s expected cash flows. Murray Rothbard (p. 489) shows that the present value of an investment project is completely dependent on the size of the expected cash flows, the timing of the expected cash flows, and the interest rate.3 To demonstrate, Alvin Hansen offers the following numerical example: “Consider the case of a [wooden bridge] costing $2,000 whose life is only three years and which offers the prospect of a series of yields of $1,000 in each of three years” (Hansen, p. 118). The wooden bridge will generate cash flows of 1,000 per year for three years. If the interest rate is 10%, then the present value (PV) of the wooden bridge is 2,486.85.
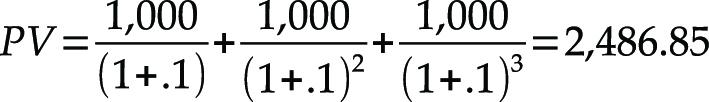

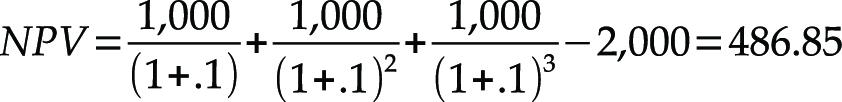
Rothbard calls the net present value (NPV) the entrepreneurial profit. The net present value equals the present value minus the price of the investment. In Hansen’s example the net present value of the wooden bridge is the present value of 2,486.85 minus the price of 2,000.

The table below summarizes Hansen’s economic calculation.
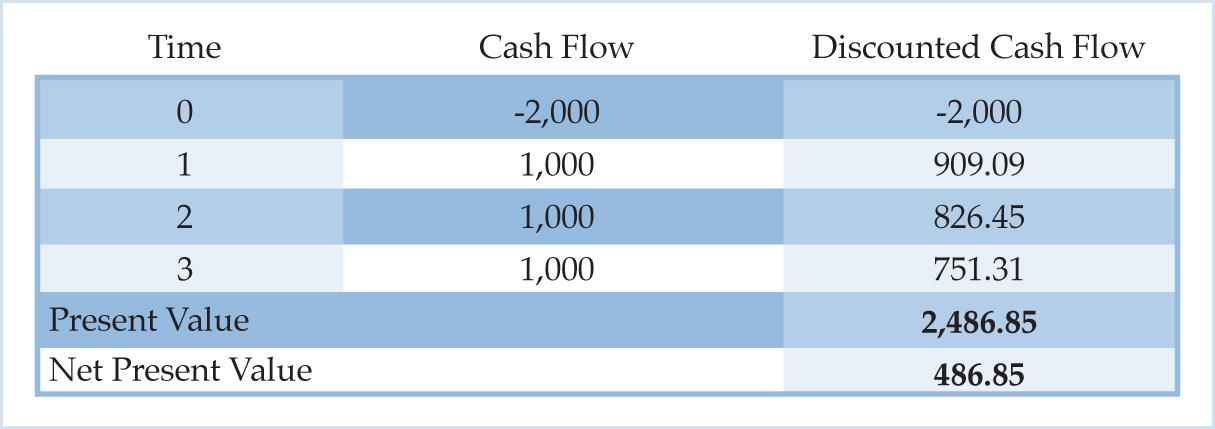
Table 1. NPV of Wooden Bridge at 10% Interest Rate
|
Competition between investors creates a tendency for the price of an investment project to equal the present value of the expected cash flows. Investors will bid up the price of an investment project when the price is below the present value, and investors will bid down the price of an investment project when the price is above the present value. Since the price of an investment project tends to equal the present value, there is a tendency for the net present value to equal zero. In Hansen’s case, the present value of the wooden bridge is 2,486.85 while the price of the wooden bridge is only 2,000. The net present value is 486.85. Other investors will be drawn to this entrepreneurial profit. Competing investors will enter the market and bid up the price of the wooden bridge to 2,486.85 where the net present value is zero. Competition between investors creates a tendency for the net present value of an investment project to equal zero.
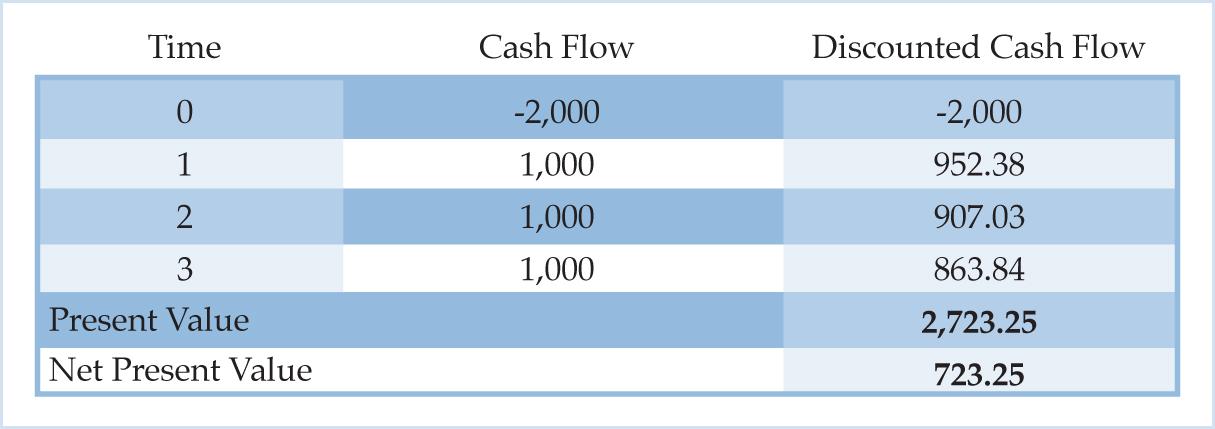
There is an important negative relationship between the interest rate and the present value of an investment project. All else equal, the present value of an investment project increases as the interest rate falls. In Hansen’s example suppose the interest rate is 5% instead of 10%. In this case the expected cash flows are discounted at 5%. Since the expected cash flows are discounted at a lower rate, the present value increases from 2,486.85 to 2,723.25.
Table 2. NPV of Wooden Bridge at 5% Interest Rate
Image

|
All else equal, the net present value of an investment project increases as the interest rate falls. In Hansen’s example the net present value increases from 486.85 to 723.25 when the interest rate falls from 10% to 5%. The NPV schedule lists a project’s net present value at various interest rates. Table 3 is the NPV schedule of the wooden bridge, and it shows that the net present value of the wooden bridge increases as the interest rate falls.
Table 3. Wooden Bridge NPV Schedule
|
The NPV schedule can be represented graphically. A continuous graph of the NPV schedule is called the NPV profile. In Figure 1, the vertical axis shows the interest rate and the horizontal axis shows the net present value. The NPV profile shows the net present value of an investment project at different interest rates.
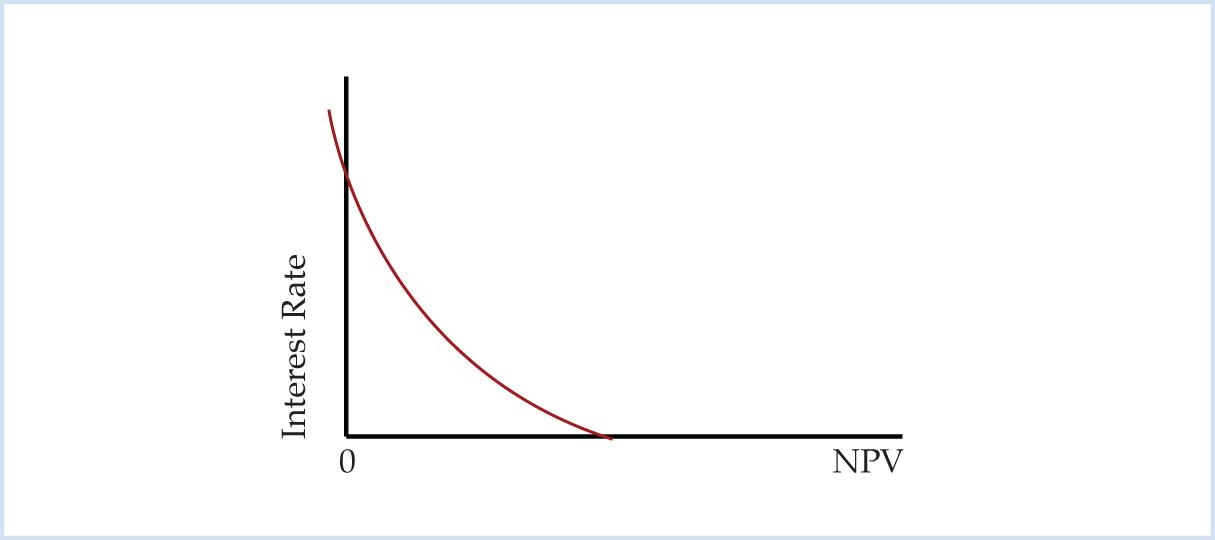
Figure 1. NPV Profile
|
The NPV profile has three properties. First, the NPV profile slopes downward from left to right. This indicates that the net present value increases as the interest rate falls. Second, the NPV profile is curved so that the NPV profile becomes flatter as the interest rate falls. Third, the NPV profile intersects the interest rate axis at the point where the NPV is zero.
The net present value is used to compare and rank competing investment projects in the present value approach to economic calculation. It is necessary to introduce another investment option to show how the interest rate affects net present value rankings. Suppose Hansen can build a more durable bridge by using steel instead of wood. The steel bridge generates the same size cash flows as the wooden bridge, but the steel bridge has a longer period of production and a longer life than the wooden bridge. The price of the steel bridge is 5,000. Starting in time three, the steel bridge will generate a 1,000 cash flow every year until time ten. Table 4 is the steel bridge’s cash flow table and it shows that, compared to the wooden bridge, the steel bridge is a long-term investment project.
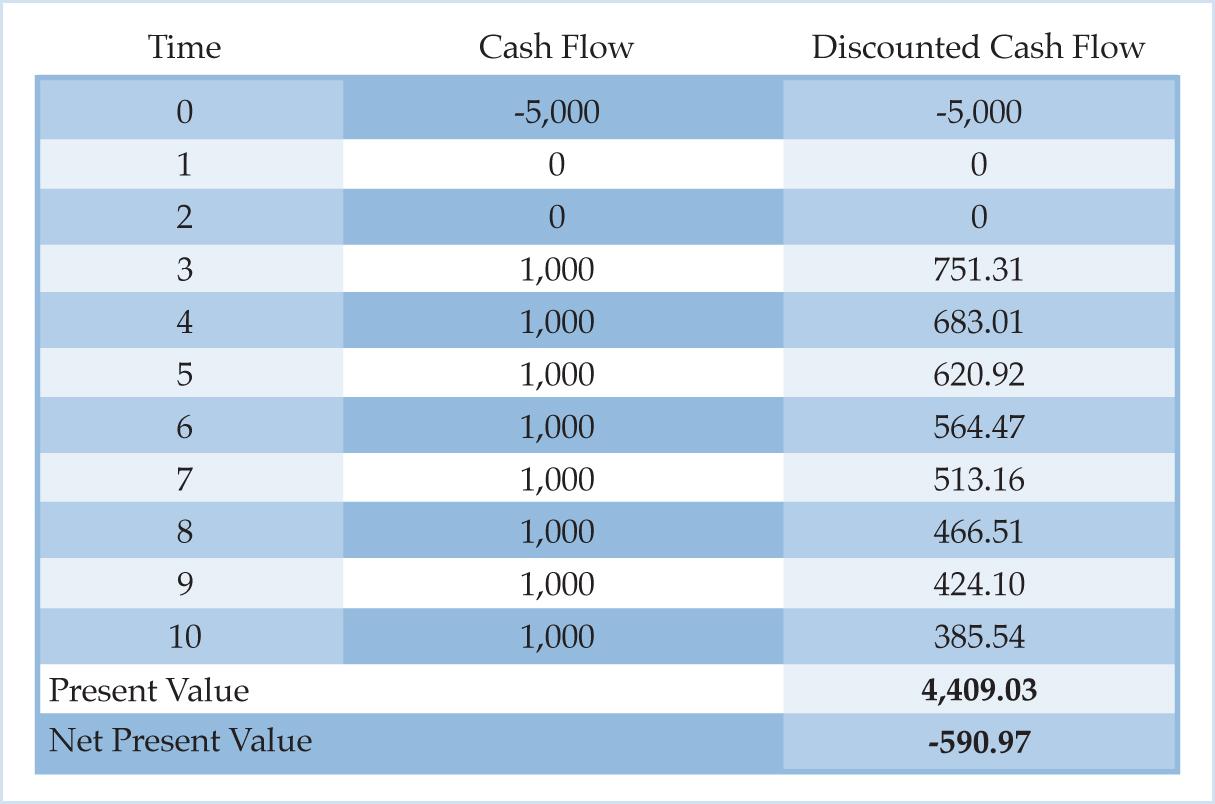
Table 4. NPV of Steel Bridge at 10% Interest Rate
|
Like the wooden bridge, the net present value of the steel bridge depends on the interest rate. Table 5 lists the net present value of both the wooden bridge and steel bridge at various interest rates.
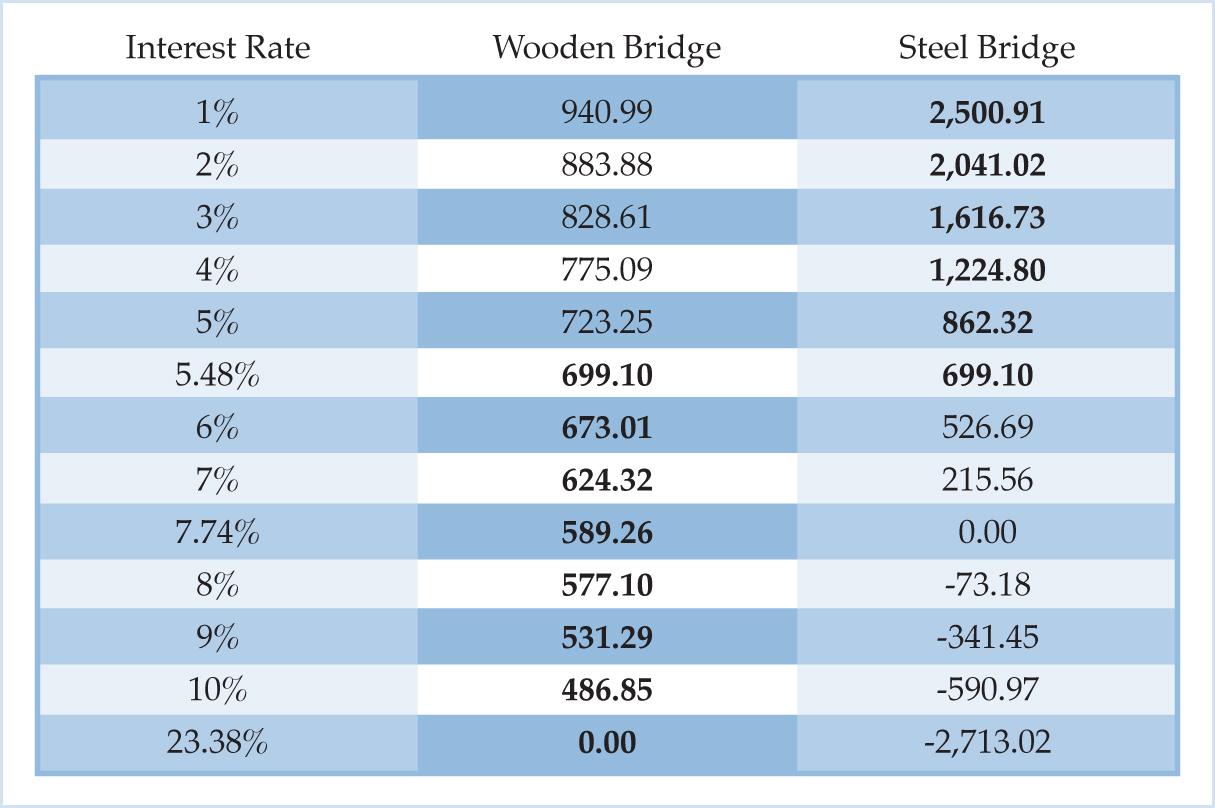
Table 5. Wooden and Steel Bridge NPV Schedule
|
Wealth maximizing investors use the net present value to rank investment projects. According to the NPV rule, wealth maximizing investors give the highest ranking to the investment option with the highest net present value. Table 5 shows that net present value rankings depend on the interest rate. The wooden bridge has a higher NPV ranking when the interest rate is greater than 5.48%, but the steel bridge has a higher NPV ranking when the interest rate is less than 5.48%. In this example, 5.48% is called the crossover rate because the net present value of the steel bridge equals the net present value of the wooden bridge when the interest rate is 5.48%. The crossover rate is the interest rate at which the projects’ net present values are equal. Fisher calls the crossover rate the rate of return over cost: “This hypothetical rate of interest which if used in calculating the present worth of the two options compared would equalize them or their differences (cost and return) may be called the rate of return over cost” (Fisher, p. 155).
NPV profiles can also be used to illustrate how NPV rankings depend on the interest rate. The easiest way to depict how the interest rate affects NPV rankings is by putting both NPV profiles on the same diagram.4
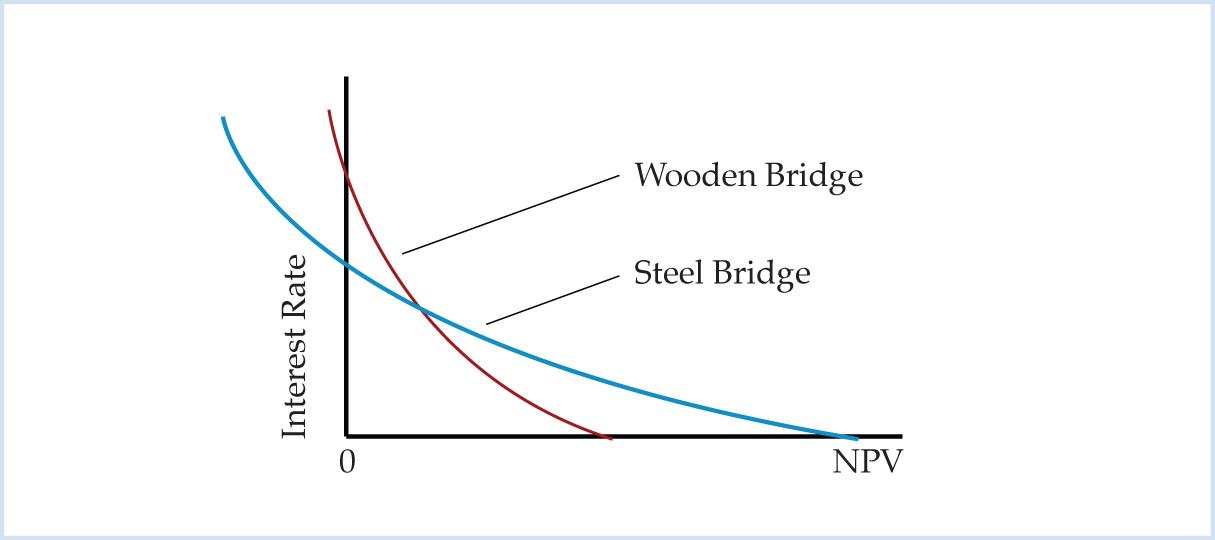
Figure 2. NPV Diagram
|
The crossover rate is the interest rate at which the two NPV profiles cross. The wooden bridge has a higher NPV ranking when the interest rate is above the crossover rate, and the steel bridge has a higher NPV ranking when the interest rate is below the crossover rate. The two profiles cross because the steel bridge has a flatter profile than the wooden bridge. The steel bridge’s flatter NPV profile reflects that the net present value of the steel bridge is more interest rate sensitive than the net present value of the wooden bridge. When the interest rate changes by a given amount, the percentage change in the net present value of the steel bridge is greater than the percentage change in the net present value of the wooden bridge. In general, long-term projects are more interest rate sensitive than short-term projects.
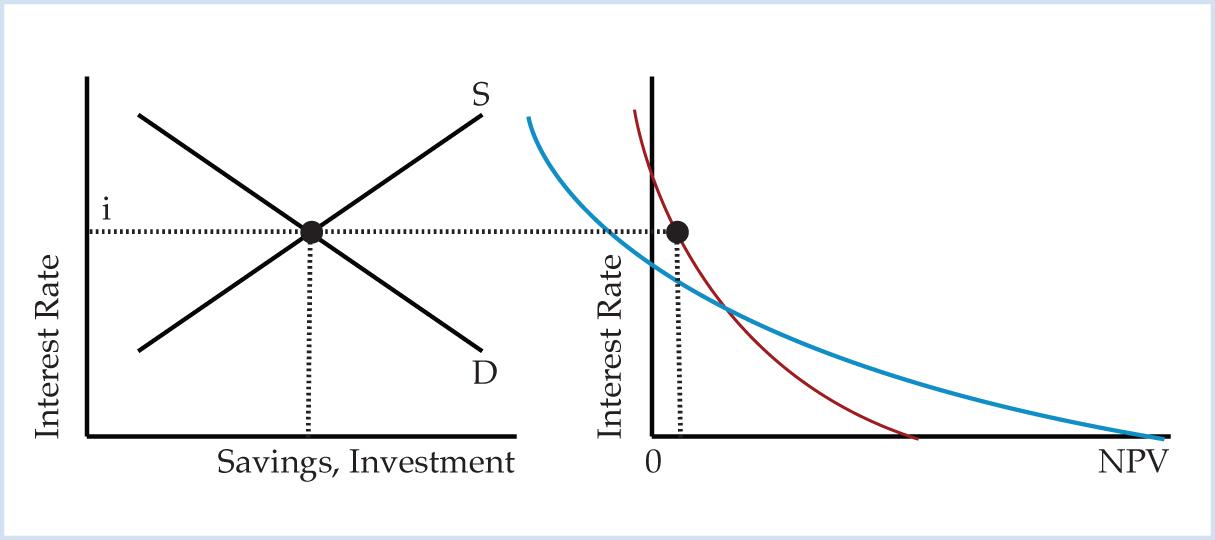
The interest rate regulates the intertemporal allocation of resources in the present value approach to economic calculation. To demonstrate, Figure 3 combines the NPV diagram and the loanable funds diagram. In Figure 3, the interest rate determined in the loanable funds market is greater than the crossover rate, so the wooden bridge has a higher NPV ranking. In this case the investor will allocate resources to the wooden bridge.
Figure 3. Loanable Funds and NPV Diagram
|
Now suppose there is a change in consumer preferences so that consumers save more and consume less. The increase in the supply of savings causes the supply of loanable funds curve to shift to the right, from S to S’. The increase in saving reduces the interest rate and increases the amount of investment.
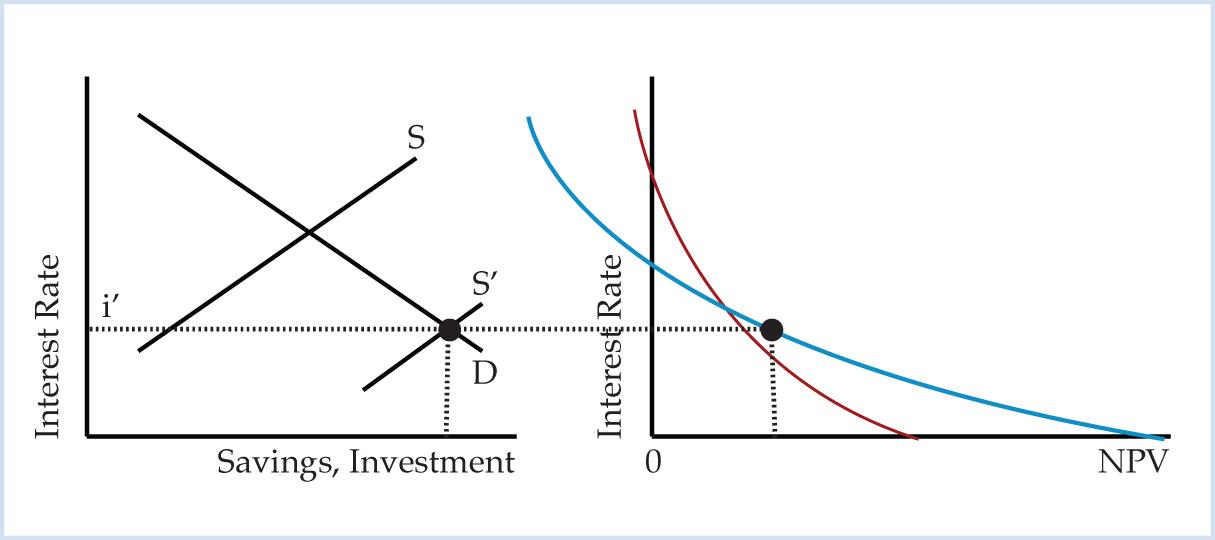
Figure 4. Increase in Saving
|
Figure 4 shows that the increase in saving by consumers changes the investor’s NPV rankings. At the lower interest rate the NPV rankings tell the investor to allocate resources to the steel bridge. The lower interest rate changes the NPV rankings because “The price of a factor which can be used in most early stages and whose marginal productivity there falls very slowly will rise more in consequence of a fall in the rate of interest than the price of a factor which can only be used in relatively lower stages of production or whose marginal productivity in the earlier stages falls very rapidly” (Hayek, p. 263). Figure 4 shows how the interest rate coordinates the actions of consumers, savers, and investors by adjusting investors’ NPV rankings to reflect changes in the saving behavior of consumers.
In the present value approach the interest rate determines the intertemporal allocation of resources. The interest rate is the price signal that “tells businessmen how much savings are available and what length of projects will be profitable” (Rothbard, p. 997). The interest rate tells the investor, through his NPV rankings, whether consumers prefer short-term or long-term investment projects. Figure 3 illustrates that resources are allocated to the short-term project when the interest rate is high; Figure 4 illustrates that resources are allocated to the long-term project when the interest rate is low. Figure 4 shows how a lower interest rate resulting from an increase in saving changes NPV rankings so that investors allocate resources into longer, more interest rate sensitive investment projects.
MARGINAL EFFICIENCY OF CAPITAL
John Maynard Keynes advocates the rate of return approach to economic calculation. In the rate of return approach investors use the marginal efficiency of capital (MEC) to rank investment projects. Keynes defines the marginal efficiency of capital as the “rate of discount which would make the present value… equal to its supply price” (Keynes, p. 135).5 In Hansen’s example, the marginal efficiency of capital is the discount rate which makes the present value of the wooden bridge equal 2,000. In other words, the marginal efficiency of capital is the discount rate which makes the NPV equal zero.
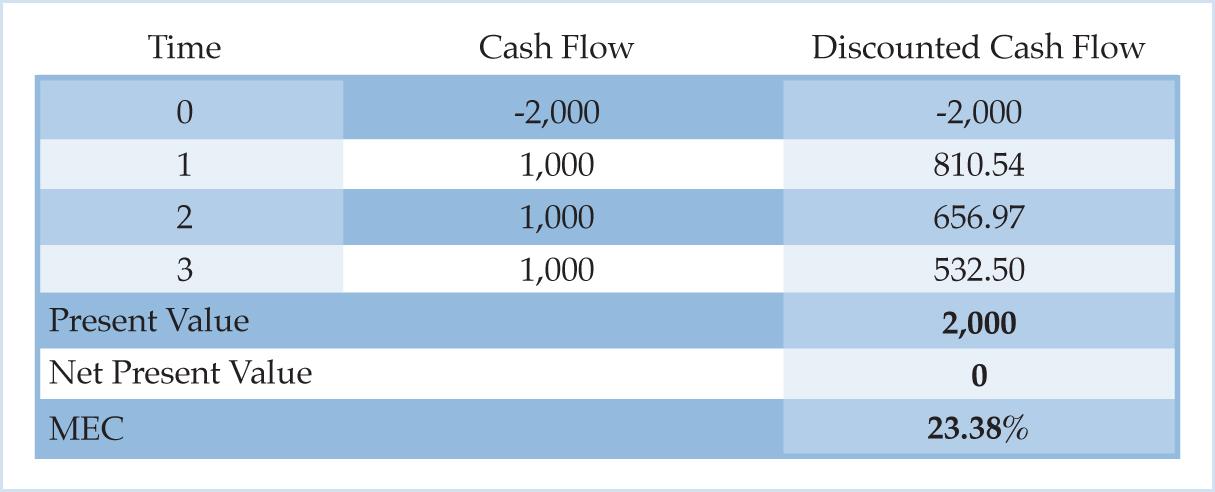
Table 6. Marginal Efficiency of Capital
|
The marginal efficiency of capital of the wooden bridge is 23.38%. When the expected cash flows from the wooden bridge are discounted at 23.38%, the present value equals the 2,000 supply price of the bridge. Put differently, the net present value is zero when the project’s expected cash flows are discounted at 23.38%. This can be seen using the NPV schedule. Table 7 shows that the net present value declines as the interest rate rises, and finally equals zero when the interest rate is 23.38%:
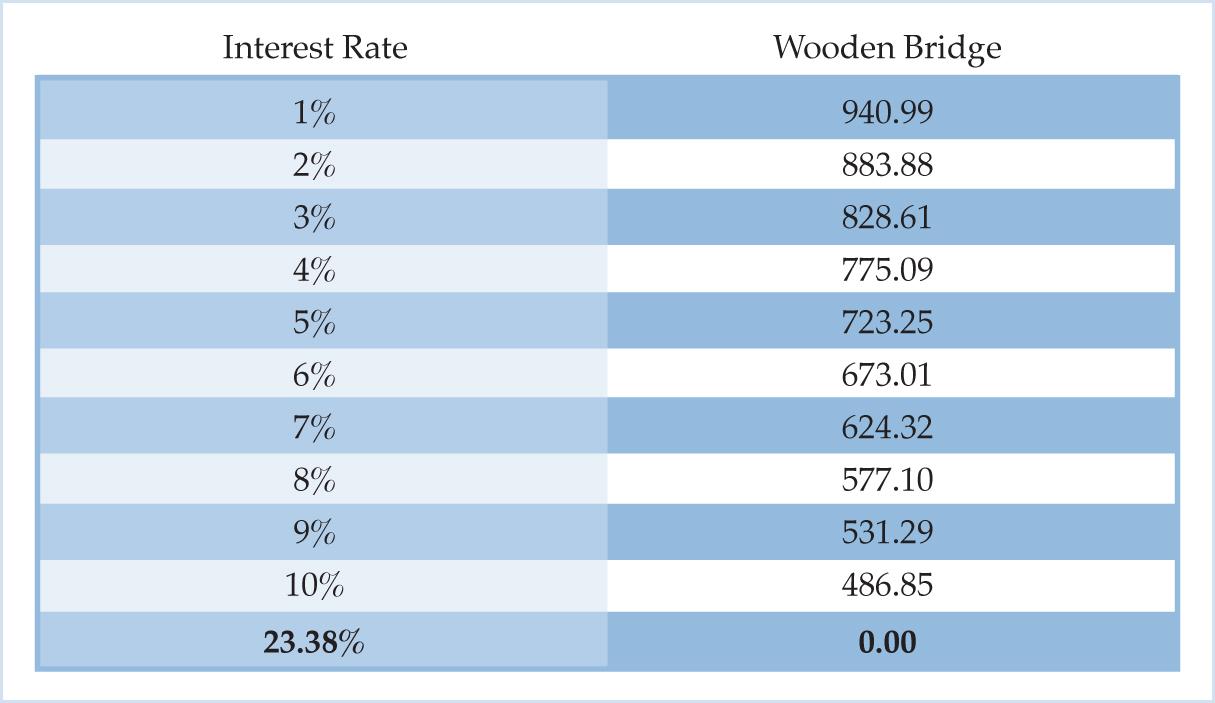
Table 7. NPV Schedule with MEC
|
The marginal efficiency of capital can also be found on the NPV profile. Since the marginal efficiency of capital is the discount rate that makes the net present value equal zero, the marginal efficiency of capital is the point at which the NPV profile intersects the y-axis.6
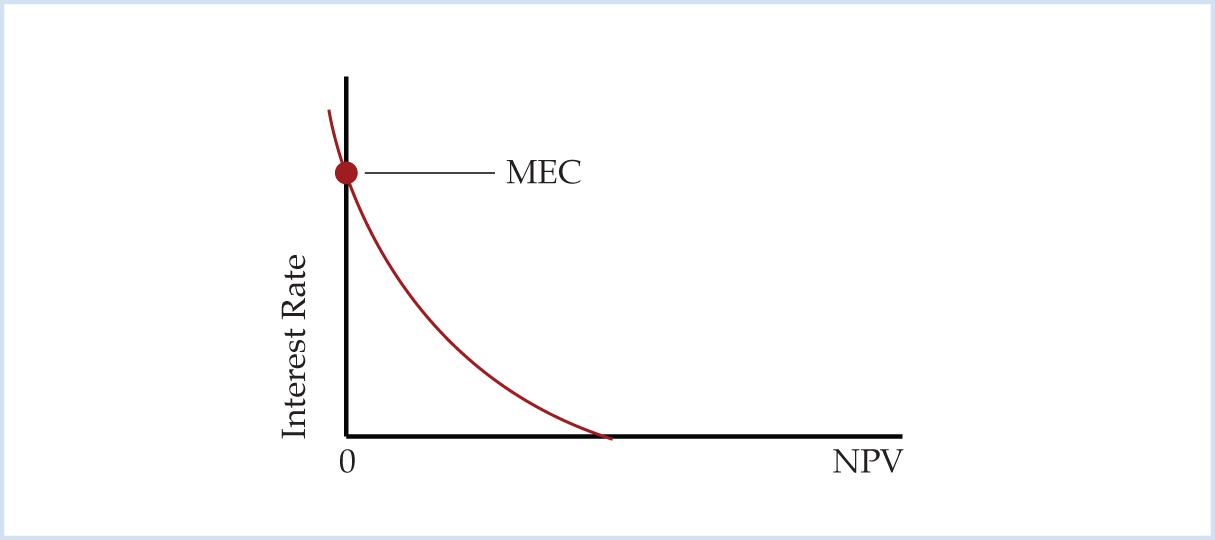
Figure 5. Marginal Efficiency of Capital
|
In the Keynesian rate of return framework investment decisions are made by comparing the marginal efficiency of capital to the interest rate. The MEC rule is to accept an investment project if the marginal efficiency of capital is greater than the interest rate. Put differently, the MEC rule is to accept an investment project if the rate of return is greater than the cost of capital. In Hansen’s example an investor will only build the wooden bridge if the interest rate is less than 23.38%. Conversely, The MEC rule is to reject an investment project if the marginal efficiency of capital is less than the interest rate. In Hansen’s case, an investor will reject the wooden bridge project if the interest rate (the cost of capital) is greater than 23.38% (the rate of return).
Expectations play an important role in Keynes’s theory and the marginal efficiency of capital is Keynes’s outlet for expectations. According to Keynes, a collapse of the marginal efficiency of capital is the cause of the economic crisis: “It is important to understand the dependence of the marginal efficiency of a given stock of capital on changes in expectation, because it is chiefly this dependence which renders the marginal efficiency of capital subject to the somewhat violent fluctuations which are the explanation of the Trade Cycle” (Keynes, p. 143). The marginal efficiency of capital is completely determined by the investor’s expectations about the size and timing of future cash flows, so the marginal efficiency of capital collapses when there is a collapse in cash flow expectations. To demonstrate, suppose Hansen reduces the cash flow forecast because his expectations suddenly become more pessimistic. The size of the expected cash flows drops from 1,000 to 750.
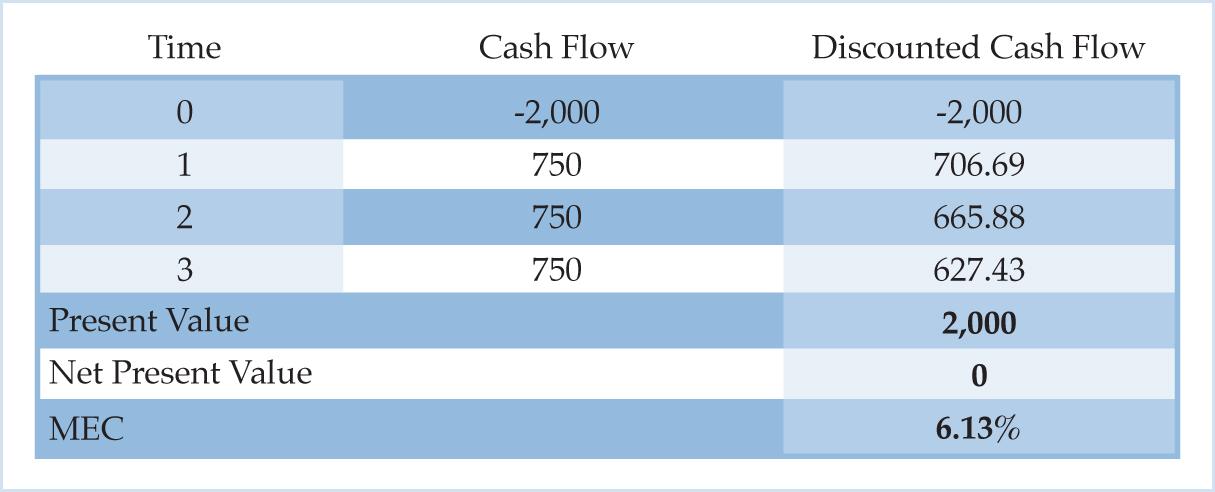
Table 8. Collapse of MEC
|
The marginal efficiency of capital collapses from 23.38% to 6.13% when the cash flow forecast is revised downward. The present value and the net present value do not change after the collapse in cash flow expectations. The present value is still 2,000 and the net present value is still zero after the drop in cash flow expectations. This example illustrates that Keynes views “the offering price of the capital good as a given, an unchanging, constant amount, even when entrepreneurs’ profit outlook varies” (Huerta de Soto, p. 555).
The most important problem with the marginal efficiency of capital is that it contradicts the wealth maximizing net present value criterion. Keynes (p. 137) and Hansen (p. 118) both erroneously claim that the rate of return approach is identical to the present value approach. The NPV diagram shows that the rate of return approach and the present value approach are related, but they are not identical. According to John Hicks, “Keynes had three elements in his theory: the marginal efficiency of capital, the consumption function, and liquidity preference” (Hicks, p. 142). All of these elements are captured by combining the Keynesian IS-LM diagram with the NPV diagram.
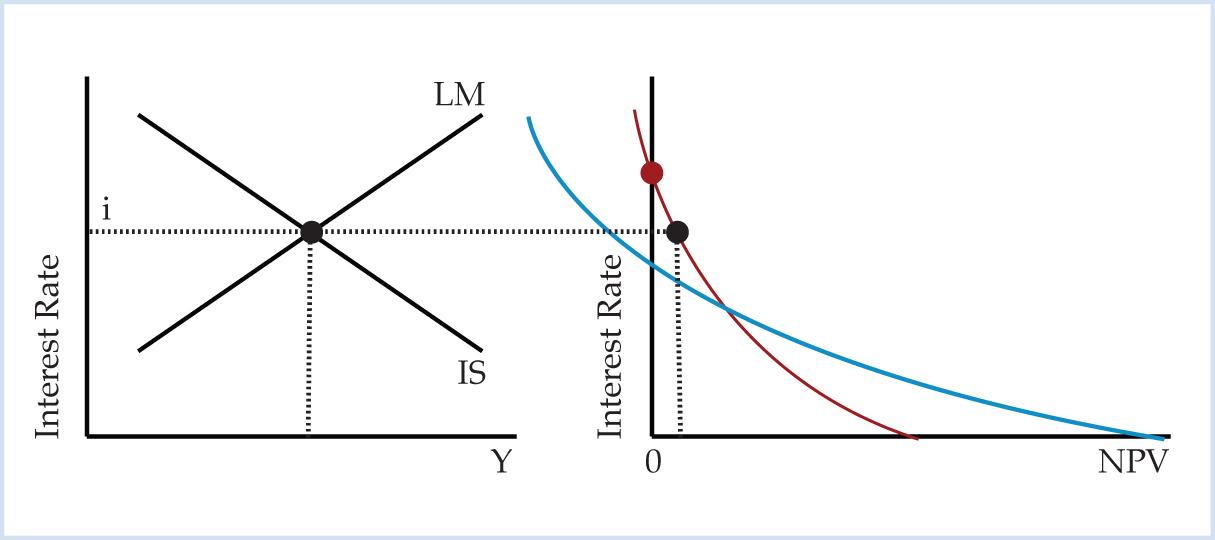
Figure 6. IS-LM and NPV Diagram
|
In Figure 6 the MEC criterion and NPV criterion yield identical results. The MEC rule is to assign the highest ranking to the project with the highest marginal efficiency of capital. Table 5 shows that the wooden bridge (23.38%) has a higher marginal efficiency of capital than the steel bridge (7.74%). In Figure 6 the wooden bridge’s NPV profile intersects the y-axis at a higher point than the steel bridge’s NPV profile, so the wooden bridge has a higher MEC ranking than the steel bridge. Since the interest rate determined in the IS-LM panel is greater than the crossover rate, the NPV criterion also ranks the wooden bridge above the steel bridge. Figure 6 and Table 5 illustrate that the net present value and marginal efficiency of capital give identical rankings when the interest rate is greater than the crossover rate.
Now suppose there is a change in consumer preferences so that consumers increase saving by reducing consumption. In the Keynesian IS-LM model, an increase in saving causes the IS curve to shift to the left, from IS to IS’. An increase in saving lowers both the interest rate and income.
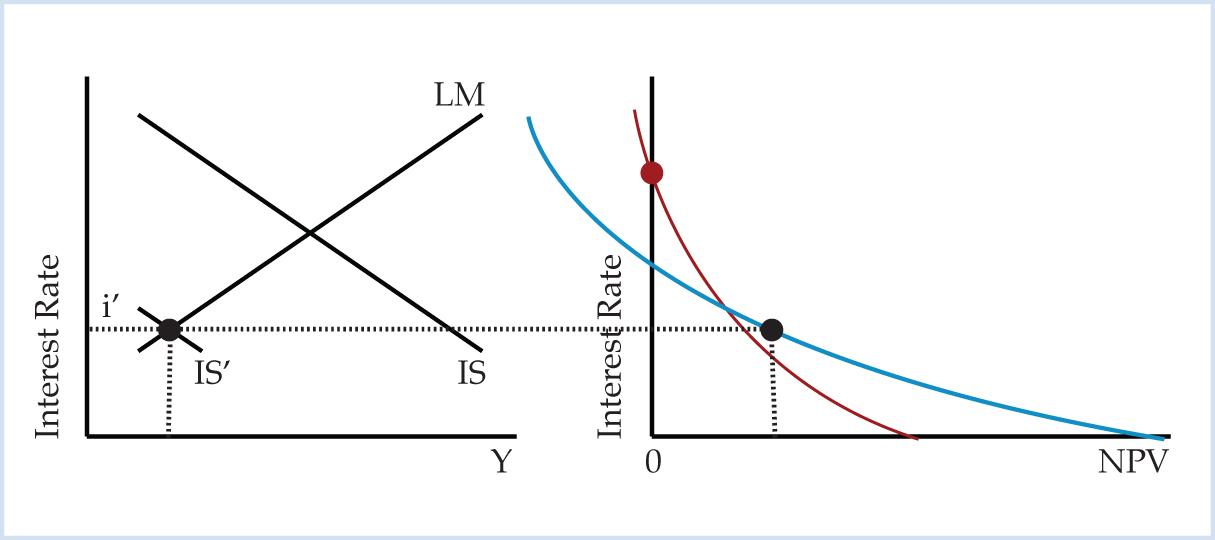
Figure 7. Increase in Saving in the Keynesian Framework
|
In Figure 7 the MEC criterion and NPV criterion yield contradictory results. Since MEC rankings do not depend on the interest rate, a lower interest rate does not change MEC rankings. At the lower interest rate the wooden bridge has a higher ranking according to the MEC criterion, but the steel bridge has a higher ranking according to the NPV criterion. The MEC rankings tell the investor to allocate resources to the smaller, less interest rate sensitive project; the NPV rankings tell the investor to allocate resources to the larger, more interest rate sensitive project.7 Figure 7 and Table 5 illustrate that MEC rankings contradict NPV rankings whenever the interest rate is below the crossover rate.
The present value approach is the wealth maximizing approach to economic calculation. Since MEC rankings contradict NPV rankings, Keynes does not provide a wealth maximizing investment demand function: “Keynes’s internal rate of return did not give an investment demand function according to the maximum present wealth criterion of choice by investors” (Alchian, p. 941). Figure 7 shows that an investor using the MEC criterion will not allocate resources to the project that maximizes wealth. The lower interest rate does not lead the investor to allocate resources to the long-term project. In the rate of return approach, the interest rate does not tell investors whether consumers prefer short-term or long-term projects. In Keynes’s theory of investment the interest rate does not regulate the intertemporal allocation of resources. Instead the interest rate is just a hurdle, or obstacle, that prevents investors from increasing investment. In the rate of return approach, a lower interest rate makes some projects which were previously unprofitable become profitable, so the volume of investment rises. By reducing the interest rate to a mere hurdle, the rate of return approach focuses attention on the volume of investment and conceals how the interest rate regulates the time dimension of investment.
The conception of the interest rate as a hurdle rate naturally leads to a monetary policy of manipulating the interest rate. Keynes advocates a monetary policy of an artificially low interest rate: “it is to our best advantage to reduce the rate of interest to that point relatively to the schedule of the marginal efficiency of capital at which there is full employment” (Keynes, p. 375).8 Following Roger Garrison (p. 165) it is possible to expand Figure 6 to include the Hayekian triangle. In Figure 8 an increase in the money supply causes the LM curve to shift to the right, from LM to LM’. An increase in the money supply lowers the interest rate and raises the level of income.
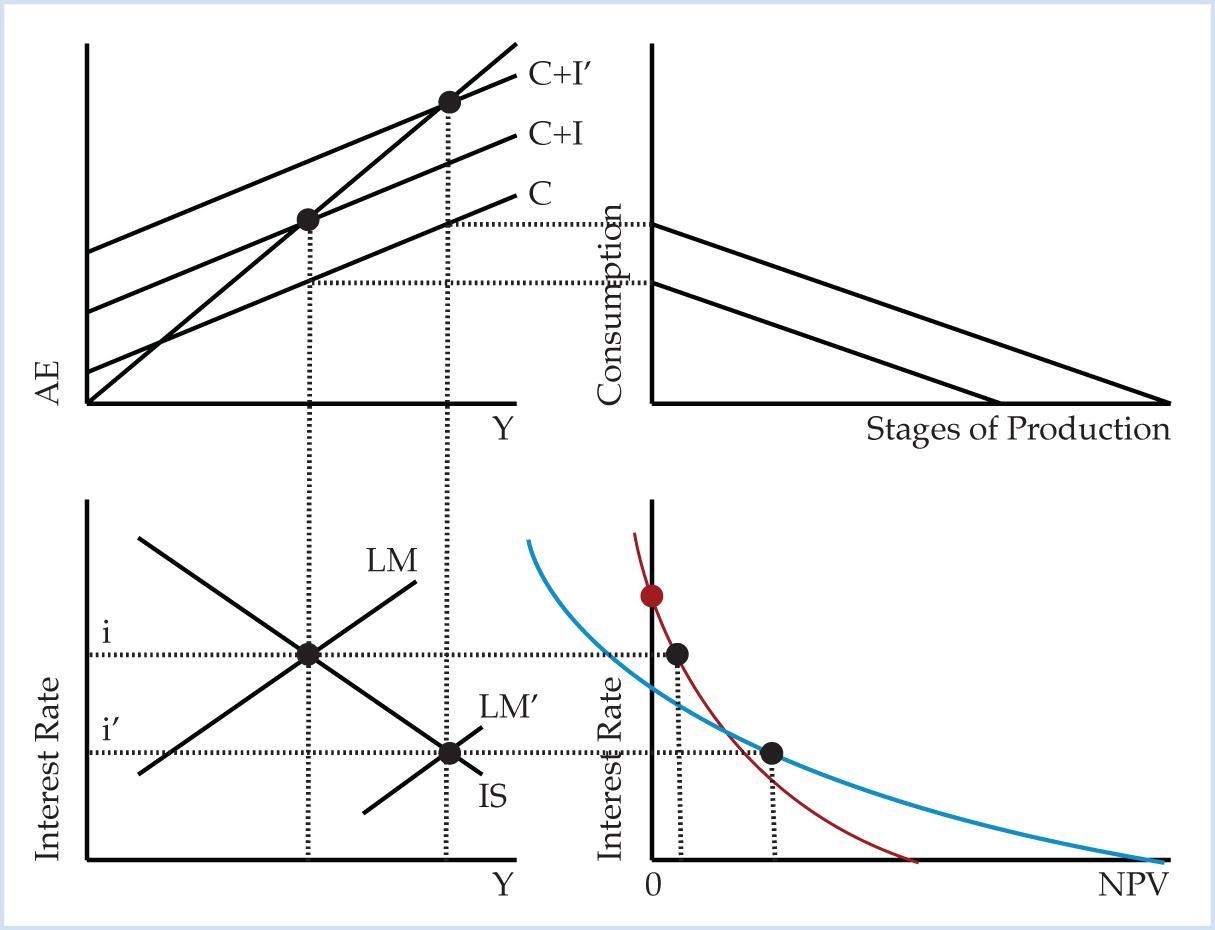
Figure 8. Artificially Low Interest Rate in the Keynesian Framework
|
The structure of production is fixed in the Keynesian system, so the increase in the money supply means “the Hayekian triangle changes in size but not in shape” (Garrison, p. 162). The fixed shape of the Hayekian triangle indicates that the interest-rate effect is absent in Keynes’s theory. Consequently, an artificially low interest rate does not initiate an allocation of resources into long-term projects. The NPV diagram also depicts that the interest-rate effect is absent in the Keynesian theory. The increase in the money supply pushes the interest rate below the crossover rate, but MEC rankings still favor the short-term project. Since MEC rankings do not depend on the interest rate, an artificially low interest rate does not cause the investor to allocate resources into the longer, more interest rate sensitive investment project. The NPV diagram and the fixed Hayekian triangle are mutually reinforcing ways of showing that the interest rate does not regulate the intertemporal allocation of resources in Keynes’s theory.
The NPV diagram reinforces the Austrian critique of Keynes’s monetary policy of manipulating the interest rate. In the Austrian theory an artificially low interest rate results in the intertemporal misallocation of resources. In the capital-based framework (Garrison, p. 69) the supply of loanable funds curve shifts to the right, from S to Sm, when the central bank expands the supply of loans.
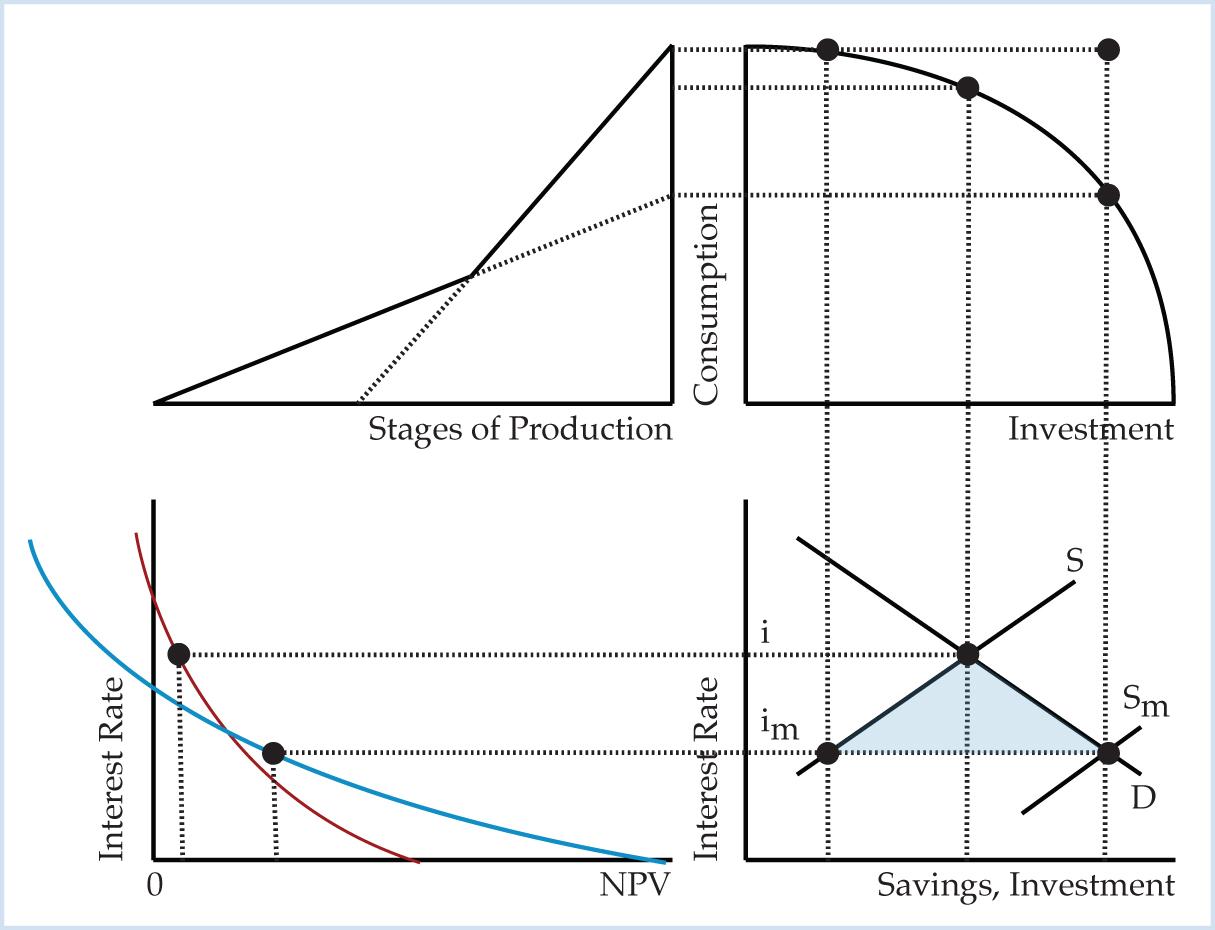
Figure 9. Artificially Low Interest Rate in the Capital-Based Framework
|
The loanable funds diagram shows that the central bank creates a double disequilibrium in the loanable funds market when it expands the supply loans.9 At the artificially low interest rate the quantity of loans demanded for investment is greater than the quantity of real savings supplied. In short, investment is greater than savings. The fall in saving means consumption rises, so the wedge between saving and investment depicted in the loanable funds market causes the economy to produce at a level outside the production-possibilities frontier (PPF). The simultaneous increase in investment and consumption shown on the PPF also plays out on the Hayekian triangle:
The tug-of-war between investors and consumers that sends the economy beyond the PPF pulls the Hayekian triangle in two directions…. investors find the longer-term investment projects to be relatively more attractive. A less steeply sloped hypotenuse illustrates the general pattern of reallocation in the early stages of the structure of production…. At the same time, income earners, for whom the lower interest rate discourages saving, spend more on consumption. A more steeply sloped hypotenuse illustrates the general pattern of reallocation in the final and late stages of production…. In effect, the Hayekian triangle is being pulled at both ends (by cheap credit and strong consumer demand) at the expense of the middle—a tell-tale sign of the boom’s unsustainability. (Garrison, p. 72)
The NPV diagram shows that central bank loan expansion causes entrepreneurial error by falsifying net present value calculations. In the NPV diagram, central bank loan expansion pushes the interest rate below the crossover rate and reverses the NPV rankings: “the drop in the interest rate falsifies the businessman’s calculation…. They make some projects appear profitable and realizable which a correct calculation, based on the interest rate not manipulated by credit expansion, would have shown as unrealizable” (Mises, p. 550). The NPV rankings are false because they do not accurately reflect consumer preferences. The falsified NPV rankings tell the investor that consumers prefer the long-term project, but consumers actually prefer the short-term project. The investor commits an entrepreneurial error by allocating resources to the project that will not satisfy the most urgent needs of the consumers. This intertemporal misallocation of resources into long-term projects is called malinvestment. The artificially low interest rate does not just affect the representative investor-entrepreneur in the NPV diagram. Since the interest rate is the universal NPV input, the artificially low interest rate causes a universal falsification of NPV rankings in favor of longer, more interest rate sensitive projects. In the Austrian theory, the universal falsification of NPV rankings causes a massive cluster of investor error. The NPV diagram and the Hayekian triangle are mutually reinforcing ways of showing that an artificially low interest rate results in an unsustainable economic boom.
- 1Edward W. Fuller (Edward.W.Fuller@gmail.com), MBA, is a research consultant at SIG.
- 2The distinction between the present value approach and the rate of return approach comes from Lorie and Savage (p. 237) and Solomon (p. 124). Both approaches are used widely in practice. Graham and Harvey (p. 33) found that 75% of the financial managers in their study use the net present value to rank investment projects. They also found that 76% of the managers in their study use the marginal efficiency of capital.
- 3Rothbard uses different terminology to describe the present value approach to economic calculation. The term cash flow is identical to the marginal value product (MVP). The term discounted cash flow is identical to the discounted marginal value product (DMVP): “The capitalized value of the capital good is the sum of the future DMVPs, or the discounted sum of the future MVPs. This is the present value of the good, and this is what the good will sell for on the capital market” (Rothbard, p. 491).
- 4See Alchian (p. 939) and Lorie and Savage (p. 237) for more on the NPV diagram.
- 5Keynes (p. 135) calls an investment’s expected cash flows the prospective yield. Today the marginal efficiency of capital is better known as the internal rate of return.
- 6The marginal efficiency of capital cannot be used in many situations. Lorie and Savage (p. 237) and Solomon (p. 127) show that projects with nonnormal cash flows will have multiple MECs. There are also situations in which the marginal efficiency of capital does not exist. Therefore, the marginal efficiency of capital cannot be the basis of a general theory of investment.
- 7The marginal efficiency of capital favors small, short-term projects. Alchian (p. 941) and Solomon (p. 126) show that MEC calculations assume that the project’s cash flows are reinvested at the marginal efficiency of capital. In contrast, NPV calculations assume that the project’s cash flows are reinvested at the interest rate. The marginal efficiency of capital’s reinvestment rate assumption penalizes large, long-term investment projects.
- 8The Keynesian liquidity preference theory of the yield curve is incompatible with the marginal efficiency of capital. The marginal efficiency of capital requires that all cash flows are discounted at the same rate, while the liquidity preference theory of the yield curve requires that each cash flow is discounted at a different rate depending on the time to maturity.
- 9The loanable funds market must be in equilibrium for the goods market to be in equilibrium. The double disequilibrium created in the loanable funds market by central bank loan expansion means the goods market cannot be in equilibrium either. One problem with the Keynesian IS-LM model is that it does not depict the double disequilibrium in the loanable funds market created by central bank loan expansion.



















