Abstract: Karl-Friedrich Israel (2018) sees “obvious tension” in a book chapter (Salerno 2018) in which I argue that the Hicksian income effect plays no role in the causal-realist approach to the demand curve. Israel’s reconstructed “wealth effect” is an effort to solve this perceived problem. This comment addresses the expositional gap in my analysis, and resolves the perceived tension. I then outline the problems with Israel’s proposed solution, which involves a wholesale reconstruction of demand theory that, in the end, implies a denial of the law of demand.
income effect — demand curve — austrian economics
JEF Classification: B53, D11
Joseph T. Salerno (salerno@mises.org) is Academic Vice President of the Mises Institute and John V. Denson II Endowed Professor in the Department of Economics at Auburn University.
1. INTRODUCTION
In his article, “The Income Effect Reconsidered,” Karl-Friedrich Israel (2018) perceives a tension in a book chapter (Salerno 2018) in which I argue that the Hicksian income effect plays no role in the causal-realist approach to the demand curve. In section 2, I address the ambiguity in my exposition which leads to this perceived tension and show how it can be readily resolved. Section 3 presents a critical analysis of Israel’s attempt to solve the problem by drastically minimizing the substitution effect in favor of a reconstructed “wealth effect,” which Israel (2018, 384) claims is “more fundamental” to demand analysis. In section 4, I consider Israel’s reformulation of the wealth effect in more detail and argue that it implies a denial of the law of demand. Section 5 offers concluding remarks.
2. THE CAUSAL-REALIST DEMAND CURVE: A CLARIFICATION OF ASSUMPTIONS
When I derived the demand curve in my original article I assumed that the following remained constant: 1. the buyer’s value scale; 2. the prices of all other goods; 3. the buyer’s stock of money balances; and 4. the purchasing power of money. The third and fourth assumptions together imply that the buyer’s real money balances are constant. I argued that the stock of real money balances must remain unchanged for units of money to attain an ordinal ranking against goods on the value scale. If the purchasing power of money and hence the stock of real money balances were permitted to vary as the money price of the good in question changed, the buyer would not be able to compare the marginal utility of goods against that of money, and a demand curve based strictly on the law of marginal utility could not be traced out. I thus maintained that there is no “income” or, more accurately, “purchasing-power” effect because the value of money does not increase (decrease) as the price of a good falls (rises) along the demand curve. I concluded that there is only a substitution effect when demand curve analysis is based on the law of marginal utility.
Israel argues that, as stated, my conclusion contradicts my second assumption that the prices of all other goods remain constant. As Israel (pp. 380–81) puts it,
[W]henever some money price is allowed to change ceteris paribus, it has a direct effect on the purchasing power of money. When a money price increases along the demand curve, then the exchange value of money and hence its purchasing power decreases, and vice versa. If, however, the demand curve for a specific good is itself contingent on the purchasing power of money, a price change along a given demand curve is contradictory as it destroys the underlying assumption on which the demand curve is based.
It was to avoid just such a contradiction that I explicitly stated that it is the ex ante or anticipated purchasing power of money today—based on the individual’s experience of yesterday’s structure of money prices—that is assumed constant. The expected purchasing power of money is used to establish the individual’s marginal utility ranking of money relative to goods that is relevant to today’s market activities. From this value ranking of goods and money is derived the individual demand curve for a particular good.
Israel (2018, 381) recognizes my inclusion of the temporal element in the analysis but rejects it as “unconvincing.” I see now that there is an expositional gap in my analysis that requires repair, but I reject Israel’s proposed solution, which involves a wholesale reconstruction of demand theory that has not been thought out to its logical conclusion. Before proceeding to evaluate Israel’s attempt to resolve the “obvious tension” in my argument, let me present the simple and obvious solution that is ready to hand.
In order to maintain the expected purchasing power of money constant along the demand curve it is necessary only to restrict my second ceteris paribus assumption to the prices of closely related goods and to interpret the fourth assumption as implying that the general prices of all other goods move inversely to the price of the good in question so as to offset the change in the value of money entailed by the initial price change. This is simply another way of saying that the relation between the supply of money and the demand for money remains constant. Thus interpreted, the assumption of a constant purchasing power of money is no more unrealistic than assuming that all prices but the price of the good under consideration remain constant while the value of money varies. In fact, Milton Friedman ([1949] 1953, 51), following Marshall, considers this assumption as one—although not his preferred—way of generating the “income-compensated demand curve.” Accordingly, he assumes that the price of “the commodity in question” changes while holding the prices of “closely related commodities” constant but allowing the “average” price of “all other commodities to rise or fall with a fall or rise of the price of [the commodity in question], so as to keep the ‘purchasing power of money’ constant.”1
Revising the set of assumptions underlying my approach in this way has the virtue of enabling analysis of the substitution effect in isolation from the purchasing-power effect. From an economy-wide perspective, this demand curve construct allows the economist to analyze the effect on a good’s price of a change in its supply (a movement along the demand curve) in abstraction from the effect on its price of a change in money demand or money supply (a shift in its demand curve). For if we allow the purchasing-power effect to manifest itself when, for example, the price of a good falls along an individual’s demand curve, then it implies that either the overall demand for money in the economy has risen or supply of money has fallen.
Now this solution does not deny that a change in the price of a good may cause both a substitution effect and a wealth or purchasing-power effect. It merely permits the two effects to be analyzed separately in order to isolate the operation of the law of marginal utility. Holding the purchasing power of money constant permits the substitution effect to be portrayed as a movement along the demand curve. With respect to the purchasing-power effect, under my revised set of assumptions, we would treat this effect as we would any change that exogenously alters an individual’s real money balances, that is, as a “real balance effect.” For example, in the case of a fall in price, real balances would rise, causing a rightward shift of the agent’s demand curves for various (normal) goods including the good in question. Using this analysis, we could also show, for example, that in the case of a big enough drop in the price of an inferior good that absorbs a large part of a household’s budget, the purchasing-power effect (shift to the left of the demand curve for the inferior good) outweighs the substitution effect (a movement down along the demand curve), which would result in less of the good being purchased by the household at the lower price. This allows us to explain Giffen’s Paradox without invoking an upward-sloping demand curve.
Alchian and Allen (1977, 69) give a very similar analysis of the “income effect.” As the price of a good falls, there occurs what they call an “expenditure-releasing effect”—that is, an increase in the purchasing power of money—because less money now is spent on the good at the initial quantity demanded. This “released purchasing power” causes a rightward shift of the individual’s demand curves for (normal) goods, including the good whose price has fallen. The substitution effect is then represented as a sliding down along a higher demand curve.2
3. A CRITIQUE OF ISRAEL’S SOLUTION
Israel offers a very different resolution of the tension he perceives in my article. He suggests that what must remain constant is “the opportunity costs of expending a given sum of money in exchange for the good in question” or, more precisely, “the purchasing power of money with respect to other goods that the person values and might want to acquire.” He argues that the fulfillment of this condition will lead to the “important assumption” for deriving the demand curve, namely, a fixed ordinal ranking of money and the good in question. There are several problems with Israel’s approach.
First, a fixed ordinal ranking is exactly what results from my revised set of assumptions above. With the purchasing power of money constant, the relative ranking of units of money and units of the good demanded will remain unchanged. Second, Israel (2018, 282) is curiously reluctant to explicitly state the assumptions about the external, objective conditions that underlie the internal or subjective prerequisite for deriving the demand curve, namely, that “the subjective value of money does not vary relative to the subjective value of the good in question.” He explains his disinclination to do so by asserting that because a fixed ordinal ranking is subjective “we cannot boil this assumption further down.” But this is a non sequitur. Surely we can specify which objective conditions in the economy are or are not consistent with this assumption. For example, allowing the prices of a good’s complements and substitutes to vary would be inconsistent with maintaining intact the individual’s ordinal ranking of the good in question and money. Israel (2018, 283) seems to realize this when he acknowledges that his precondition of a fixed ranking is consistent with Hicks’s assumption that all other prices in the economy are constant. He then appears to back off such a strong assumption two sentences later by declaring, “strictly speaking, what has to be held constant for the construction of the demand schedule are the opportunity costs of expending money on the good in question, whatever the influencing factors of this subjective notion may be.” Later in his article, Israel (2018, 394, 396) seems to reverse his field yet again by explicitly using the Hicksian assumption in an example in which he derives the demand curve and then conceding in his conclusion that his own “assumption for the derivation of the demand curve essentially boils down to Hicks’s original assumption.”
Israel’s strange reluctance to clarify the assumptions he uses in deriving the demand curve is inconsistent with causal-realist analysis, which is predicated on a tight and consistent connection between single-market or “partial equilibrium” analysis and general interdependence analysis. As the prominent monetary theorist, Arthur Marget ([1938-1942] 1966, 166), pointed out:
To say that the “demand schedules for particular industries can only be constructed on some fixed assumption of the nature of demand and supply schedules of other industries” is to say nothing more than... what has come to be called “partial equilibrium” analysis is continually subject to the limitations imposed upon it by “general equilibrium” analysis of the Walrasian type.3 [Emphasis is in the original.]
In any case, Israel’s failure to fully and forthrightly state the assumptions underlying his derivation of the demand curve renders his solution inadequate at best. If he does not completely embrace Hicks’s assumption, then he needs to provide a different assumption about the constancy or variation of other prices in the economy that are required for the fixity of the ordinal ranking of money and the good in question. If he is unable to articulate an alternative assumption, then I think he is compelled to assume the constancy of the purchasing power of money as I have explained above.
This brings me to the third problem with Israel’s solution, which is closely related to the second. Israel (2018, 396) accepts my point that causal-realist demand analysis entails that “money is treated as an actual good that is valued as such and that is demanded or retained. It is not simply a numeraire.” But once it is admitted that money as a valued good plays a key role in deriving the demand curve, assumptions about its own supply and demand must be made explicit. According to Israel (2018, 380–81): “When a money price increases along the demand curve, then the exchange value of money and hence its purchasing power decreases, and vice versa.” In Israel’s analysis, therefore, a variation of the price of the good along the demand curve involves a disturbance in the market for money balances. If the price of the good in question falls, it does so because either: 1. There has been an increase in the reservation demand for money on the part of other buyers who increased their cash balances by reducing the market demand for the good; or 2. The overall supply of money in the economy has contracted with a particular incidence on those who were former purchasers and who reduce their demand for the good.
Israel neglects to state the assumption about the market for money balances necessary to his argument that the purchasing power of money changes as the price of the good in question varies along the demand curve. But once this assumption is explicitly stated, it raises the question of why the demand curve cannot be derived simply by assuming that the price of the good in question varies solely as a result of a change in relative demands for goods in the economy while leaving the market for money balances undisturbed.4 The demand curve yielded by the latter assumption, which is the one I propose above, would be different from the demand curve derived using Israel’s method of tacitly supposing changes in the market for money balances.
For Israel, the change in quantity demanded associated with the change in price thus conflates two factors: the effect of the law of marginal utility and the real balance effect. It is precisely because purchasing power and substitution effects are in reality inextricably intertwined that we assume that the purchasing power of money remains constant along the demand curve. This enables the causal-realist theorist to isolate the two effects for purposes of analysis. The effect of a price change on substituting between goods is illustrated as a movement along the demand curve; the effect of a variation of real money balances is shown as a shift of the demand curve. This analytical distinction is especially useful in explaining the step-by-step process of adjustment to a change in the money supply in a closed economy or the balance of payments in an open economy in which both effects play a crucial role (Hayek [1937] 2008, 351–66; Salerno [1984] 2010).
Marget ([1938-42] 1966, 301), an early critic of the Hicksian income effect, supports this point by arguing that the “response of a given consumer’s demand for a particular commodity” may differ depending on whether it is induced by “an increase in ‘real income’ as the result of a fall in the money price of a given commodity” or by “a change in the level of money income with money prices remaining the same.” The Hicksian approach, which is based on “the interpretation of a fall in a given money price as an increase in the ‘real income’ of income recipients,” brings with it “pitfalls” associated with the index-number problem. According to Marget ([1938–42] 1966, 301), these pitfalls are avoided by
...the ‘older’ method of dealing with the effect of a fall in a given money price in relation to income.... For, according to this method, the fall in a given money price is regarded as affecting the quantity of particular commodities demanded either by causing a movement along a given demand schedule or by changing the conformation [i.e., shape] or position of a given demand schedule. [Emphasis added].
Israel ignores such considerations of analytical practicability because, at bottom, his position rests on a single-minded quest for greater realism in the derivation of the demand curve. But the demand curve is a mental construct just like the Evenly Rotating Economy (ERE), and the assumptions for constructing both are chosen by the theorist for analytical convenience. An economy operating under the complete absence of uncertainty and change as depicted by the ERE is not only unrealistic but unrealizable and self-contradictory. And yet this construction of a static economy enables us to disentangle the dynamic real-world phenomena of profit and interest for separate causal analysis. Similarly, the individual demand curve is merely a tool of thought that permits us to disentwine and separately analyze the substitution and real balance effects of a price change. The unrealism of the assumptions of the ERE and the demand curve are irrelevant to their respective functions. After all, the Hicksian assumption that all other prices remain constant in the face of a change in the price of one good is also highly unrealistic. For it heroically assumes that a change in the market for money balances exerts its full effects in the market for a single good, while leaving all other markets for goods undisturbed. Why is it somehow less realistic to assume that the purchasing power of money remains constant along the demand curve?
In fact, realism of assumptions has nothing to do with the matter because the demand curve is a mental construct, which selectively embodies some elements of action while abstracting from others. As Mises (1998, 65, 237–38) describes it,
An imaginary construction is a conceptual image of a sequence of events logically evolved from the elements of action employed in its formation. It is the product of deduction, ultimately derived from the category of action, the act of preferring and setting aside. In designing such an imaginary construction the economist is not concerned with the question of whether or not it depicts the conditions of reality which he wants to analyze. Nor does he bother about the question of whether or not such a system as his imaginary construction could be conceived as really existent and in operation. Even imaginary constructions which are inconceivable, self-contradictory, or unrealizable can render useful, even indispensable services in the comprehension of reality....
Furthermore, as Rothbard (2009, 576 fn. 15) insightfully points out, “The constructs are imaginary because their various elements never coexist in reality; yet they are necessary in order to draw out, by deductive reasoning and ceteris paribus assumptions, the tendencies and causal relations of the real world.” Thus, the demand curve does not exist in reality because changes in prices cannot coexist with the absence of income or wealth effects. Yet the demand curve, despite the unrealism of its assumptions, is essential to grasping the separate effects on the quantity of the good demanded of a change in its own price and a change in all other factors, including the purchasing power of money, despite—or rather, because of—the fact that these factors operate together to produce a composite effect in reality. Indeed, when the fictive assumptions that underlie the derivation of the demand curve are successively dropped, we retain the truth of an inverse relationship between price and quantity demanded. We then add to it further truths utilizing shifts in the demand curve to elucidate the causal relations between the demand for a good and changes in prices of closely related goods, future price expectations, the stock of money balances, and so on. Proceeding in this manner, we achieve progressively closer approximations to an account of the full reality of the pricing process.5
Philip Wicksteed ([1933] 1957, 439–527) presented the most profound and extensive analysis of the nature and function of the demand curve encountered in the literature. He clearly recognized that the method of imaginary constructs was necessary in deriving individual demand curves, or what he called “total utility” curves. Wicksteed ([1933] 1957, 474) argued that the curves: 1. are “purely abstract,” to be derived in the absence of other causes “that might be supposed in actual experience” to change the price or quantity demanded of the good under consideration; 2. are “isolated,” in that “we cannot conceive of a system of such curves” for a given individual “to be valid simultaneously”; and 3. are not constructed so that we can “read on them the effect of a rise or fall in the consumer’s income.” All these curves can do is “represent the subjective value attached by a consumer to each increment of the commodity, or the amount he would purchase at any given price.” And yet, he asserted, “their form has a high theoretical significance.”
In particular, Wicksteed emphasized that that an individual demand curve for a commodity cannot coexist with changes in the individual’s “total resources” or “income.” Thus, for Wicksteed ([1933] 1957, 482–85), as price increases along the individual demand curve toward its intersection with the price axis, we assume the individual’s “total resources or income are to remain the same, but that this particular market is to be closed to him,” i.e., the price rise surpasses his maximum buying price for the first unit. But if income is assumed to change as a result of the price movement, the demand curve vanishes because “this will affect the whole system of his scale of preferences.” And this is true whether income varies as a result of exogenous factors or as an endogenous effect of the movement along the demand curve, because “every curve is changed by a change in the supplies of other commodities as well as that to which it specially refers.” In the phrase I emphasized in the foregoing quotation, Wicksteed is referring to the additional supply of the good purchased at a lower price due to the income effect. In considering two demand curves for the same good for the same individual under the alternative suppositions that the person is “rich” and “poor,” Wicksteed concluded, “The two curves... would have no significant relation to each other.” In other words, an income effect, which renders an individual richer or poorer, is inconsistent with the derivation of a given demand curve.
Wicksteed ([1933] 1957], 486–87) also considered the effect of changes in the expected purchasing power of money caused by a variation of price along an individual demand curve to violate ceteris paribus assumptions:
[A]n attempt to trace an individual demand curve back towards the origin [i.e., the price axis] is legitimate, and its results are interesting, suggestive, and enlightening in proportion as the condition “other things remaining the same” is observed.... [Such] curves must depend for their construction on imaginative estimates of the value we ourselves should under present conditions attach to small increments of the commodity at given margins; not on attempts to reconstruct conditions that might really raise the market price to a high figure.
Here the “conditions” that Wicksteed is referring to are those in a besieged city in which the price of a staple such as bread suddenly rises substantially due to the good’s greater scarcity. A ceteris paribus demand curve for bread cannot be constructed if, as is realistically the case, this rise in price evokes expectations of an imminent rise in the prices of related goods and an impending collapse of the purchasing power of money and shrinkage of real incomes.
Wicksteed ([1933] 1957], 487) anticipated and responded to the objection that the restrictiveness and unrealism of the underlying assumptions of the demand curve make it worthless for analysis of real-world phenomena:
It may well be asked whether a method that needs so much guarding and explaining is worth adopting at all. The answer is that the principle of declining marginal significances is absolutely fundamental. The doctrine of surplus value in the thing bought over and above the value of the price paid [i.e., consumer surplus] is an inevitable deduction from it. The awakened mind must, and as a matter of fact does, speculate upon it.... It is intimately connected with the relations of Economics to life. A want of a clear understanding of it brings perpetual confusion into our speculations and entangles the student in perplexities and contradictions.
4. ISRAEL’S WEALTH EFFECT: OVERTURNING THE LAW OF DEMAND
Israel (2018, 384–95) appears to enmesh himself in such “perplexities and contradictions” when he attempts a radical reformulation of the derivation of the demand curve based on what he terms the “wealth effect.” According to Israel (2018, 384) the wealth effect is “a type of income effect” and is “more fundamental” than the substitution effect, which manifests itself “only in cases where demand is price elastic.” Israel goes beyond the neoclassical conflation of the substitution and income effects and enshrines the wealth effect as the core of demand analysis. In his zeal for realism, Israel (pp. 396–97) characterizes the demand curve as a concept directly intuited from raw experience,
...an easy and direct illustration of a very real phenomenon that most people intuitively understand, namely, that consumers are made better off when a given good can be acquired at a lower money price. The wealth improvement with respect to the cash balance may be used to finance an increase in the quantity of the good demanded.
In lieu of a detailed analysis of the wealth effect, the explanation of which takes up more than half of Israel’s article, I will restrict myself to two general comments. First, as argued above, the demand curve, at least in causal-realist theory, is a heuristic device that is designed to elucidate the operation of the law of marginal utility in the pricing process by tracing out the effect of a change of price on the quantity demanded, while all other factors influencing the amount of the good purchased are impounded in the ceteris paribus clause. In Israel’s formulation, in contrast, the demand curve mainly illustrates the direct effect on quantity demanded of a change in wealth, albeit a change caused by a change in the price of the good itself. The wealth effect, Israel (2018, 384) asserts, “...is a direct consequence of any price change along the demand curve.” But, as Wicksteed ([1933] 1957, 474, 483–84) emphasized, one cannot “read on [demand curves] the effect of a rise or fall in the consumer’s income” because a variation in wealth “will affect the whole system of his scale of preferences.” This holds true even if wealth varies exclusively as a result of a change of the price of the good to which the demand curve “specially refers.”
This brings us to a second objection to Israel’s conception of the demand curve. While arguing that the wealth effect dominates the substitution effect in determining the shape of the demand curve, he presumes that the demand curve is downward sloping. Let us take the example that he gives of a farmer’s demand schedule for beer, which is presented in Table 1. The farmer is supposed to be initially endowed with 200 monetary units and to trade them for volume units of beer, let us say dollars and liters, respectively.6
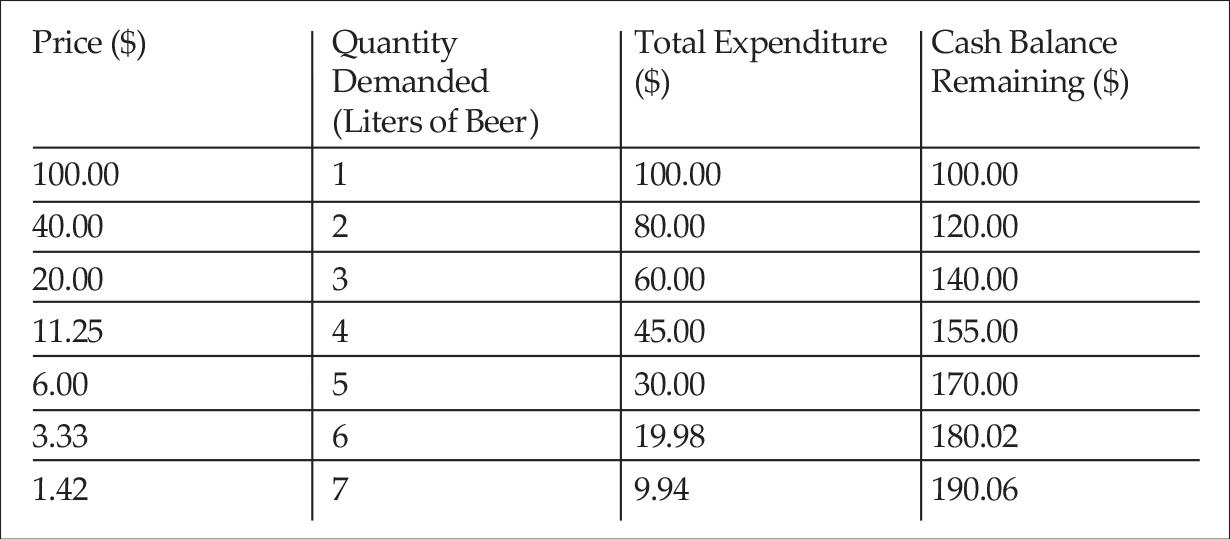
Now if we assume prices of all other goods remain constant, as Israel does, then a decline in the price of beer brings about an increase in wealth. That is, at the same quantity demanded, a lower price enables the buyer to afford more preferred combinations of beer, other goods, and retained cash balances. However, Israel’s demand schedule implies that the buyer would always either use a portion of this “released purchasing power” to increase the amount purchased of beer or maintain the quantity demanded of beer constant and expend the entire windfall on additional units of other goods or building up his cash balance or both. Israel thus illustrates the wealth effect with discrete, downward-sloping demand curves with vertical segments, as exemplified in the demand schedule in Table 1.
In causal-realist theory, however, a change in an individual’s wealth revolutionizes his preference scales and, therefore, the entire structure of his demand curves. As Wicksteed ([1933] 1957, 483) wrote:
[L]et us suppose that a man’s income increases or diminishes. This will obviously affect the whole system of his scales of preference. Possibly “pop and cockles” [i.e., clams] may completely fall out of his list of purchases, and “champagne and oysters” may appear on it; but in an ordinary case... while some modes of expenditure will probably be dropped and some almost certainly introduced, a large number will be extended.
In other words, an individual’s demand curves for a given good before and after winning $10 million in a lottery or receiving a $10,000 bonus from an employer are derived from different preference scales and therefore bear no relationship to one another. In theory, this is also true of an increase in real money balances accruing to an individual as a result of the “wealth effect” caused by a fall in price of a particular good in his budget. Thus Israel’s assumptions that the purchasing power of money is not constant along the demand curve and the wealth effect dominates the substitution effect conflict with his presumption that demand curves are always downward sloping with vertical segments. In fact, the demand curve may just as well be configured like the one depicted in Table 2 as the one in Table 1, with upward-sloping segments of the curve reflecting differences in scales of preference at varying levels of wealth. At the price of $11.25 per liter the buyer may reduce his beer consumption below the quantity demanded at $20.00 or $40.00 per liter because the additional wealth in the form of “released purchasing power” permits him to attain the higher level of satisfaction of a top tier bottle of bourbon and a beer chaser.7
At $6.00 per liter, his beer purchases increase because he is able to attain an even more preferred combination of goods and money balances that includes displaying his generosity by buying a round of beer for his friends at his local pub. A price of $3.33 per liter would put him in the position to enjoy a more preferred bundle of consumption goods and cash balances that includes one quick beer with friends and treating his wife to dinner at a new restaurant.
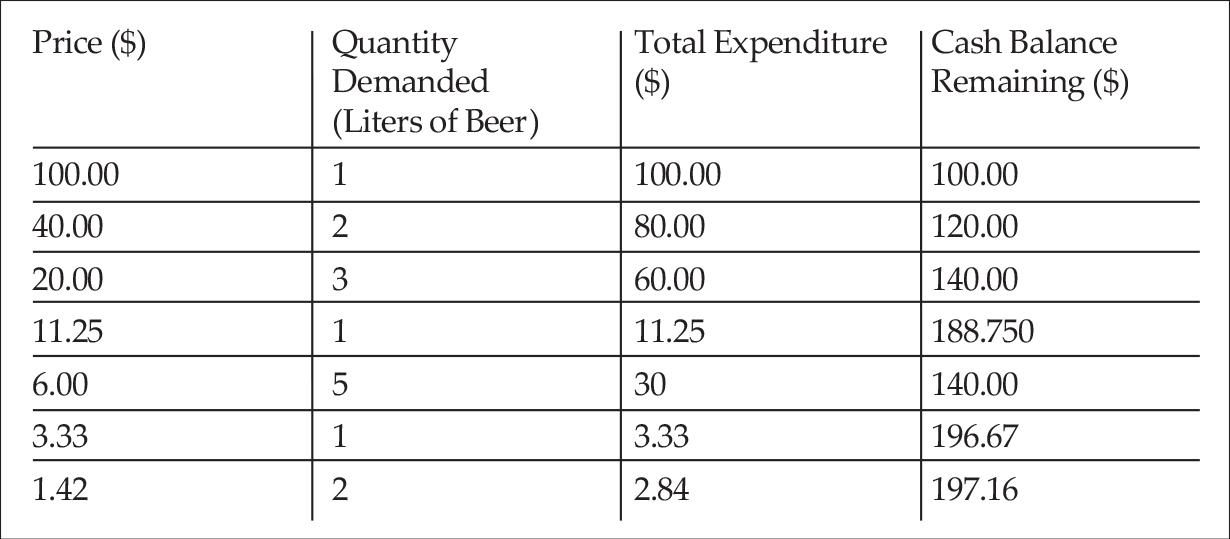
We conclude that when the wealth effect, as Israel describes it, is proposed as the fundamental concept of demand analysis, the presumption that the price of a good and its quantity demanded, ceteris paribus, move inversely to each other no longer holds. In addition, the substitution effect thus becomes completely extraneous. The latter effect is not necessary to explain the response of quantity demanded to changes in price, even along elastic segments (e.g., between $11.25 and $6.00 in Table 2) as Israel claims. It may be fully explained by the change in wealth. The substitution effect can only be offered as a definite explanation for the shape of the demand curve when “wealth” or real cash balances and, hence, the scale of preferences remain unchanged.
4. CONCLUSION
Israel is to be credited for pointing out my lapse in expounding the assumptions underlying the derivation of the causal-realist demand curve. His insightful criticism has led to what I hope is a more satisfactory exposition. However, as I have tried to demonstrate, Israel’s attempt at a wholesale reconstruction of demand theory in the space of a few pages of a comment is both unnecessary and not carefully thought out. It reflects a misleading and self-defeating quest for realism that, in the end, leads—unwittingly—to a denial of the venerable law of demand, one of the most important and useful theoretical constructs for interpreting economic reality. That said, I am not completely dismissing Israel’s conception of the wealth effect as valueless for economic analysis. But in order to persuade mundane, workaday economists of its value, he needs to reframe it strictly in terms of its analytical usefulness rather than invoking an appeal to realism as the pivot of his argument.
- 1Austrian economists would of course replace Friedman’s concept of an “average” of prices of all other commodities with that of an “array” of particular prices of all other commodities.
- 2For a similar analysis, see also Alchian and Allen (1972, 69–70) and Alchian and Allen (2018, 119–20), although these treatments do not explicitly mention the important concepts of the “expenditure-releasing effect” and “released purchasing power.”
- 3Marget ([1938–42] 1966, 170, fn. 55) is here using the term “general equilibrium analysis of the Walrasian type” in a loose sense that includes Austrian-type general interdependence analysis. He thus notes the similarity between the early 20th-century American “Austrian” price theorist Herbert J. Davenport and his “system” and that of the Lausanne school in Davenport’s “insistence in stressing the limitations set by the fact of the general interdependence of prices to [partial equilibrium] analysis.”
- 4We would of course need to assume, as mentioned above, that the change in relative demands does not affect the prices of direct substitutes and complements of the good in question but only of unrelated goods.
- 6Israel (2018) uses euros and Masskrugs.
- 7As noted above, (p. 5) Alchian and Allen (1977, 69) calculate released purchasing power as the difference between the total expenditure on the good at the initial higher price and the new lower price for the quantity demanded at the higher price. For example, based on Table 2, if the price for a liter of beer falls from $20.00 to $11.25, then total expenditure on 3 liters of beer falls from $60 at the price of $20.00 to $33.75 at the price of $11.25, yielding released purchasing power of $26.25.


