Abstract: This paper offers a synthetic and comparative assessment of the most basic Austrian macroeconomic models, i.e. the models that analyze the static forces determining the equilibrium interest rate and structure of production (monetary disequilibria and business cycles are not part of this investigation). The three models presented here are those of Böhm-Bawerk ([1889] 1959), Hayek (1936, 1941), and Garrison (2001). This review shows that these models are largely inconsistent with each other, but also that at a more general level they share several important characteristics. Finally, a tentative explanation is offered as to why there is no cumulative tradition in the Austrian School in this kind of basic macroeconomic theorizing.
JEL Classification: B13, B25, B53, E14
Key Words: hayekian trianage austrian economics business cycle macroeconomics
Renaud Fillieule (renaud.fillieule@univ-lille.fr) is Professor of Sociology at the University of Lille, France, and member of the CLERSÉ research unit (UMR CNRS 8019).
A preliminary version of this paper was presented at the Austrian Economics Research Seminar in Paris, France, May 9, 2017. The author wishes to thank Prof. Hülsmann for this invitation and the attendees for their remarks and suggestions.
INTRODUCTION
The Austrian School is best known for its subjectivist approach and for its theories of the market process and the business cycle. This paper focuses upon a less familiar but nevertheless significant topic. Prominent economists of this school have developed, over the century and a half of its existence, a series of basic macroeconomic models. These models are “basic” in the sense that they investigate the most fundamental forces operating in an economic system, leaving aside the complications due to monetary disturbances and to uncertainty. No systematic comparison between them has been provided yet, and this paper seeks to fill this gap. This kind of basic and integrated model analyzes the convergence process of a very simplified economic system towards a macroeconomic equilibrium, and investigates the macro-effects of typical changes such as technical progress, a lower or higher time preference (leading respectively to a larger or smaller saving-investment), or an increase in the number of workers. Monetary disturbances and short-term fluctuations are therefore off topic here. Three models fit these criteria in the published Austrian literature. They were respectively elaborated by (i) Böhm-Bawerk ([1889] 1959), (ii) Hayek (1936, 1941), and (iii) Garrison (2001).1 The first purpose of this paper is to provide a history of the way basic macroeconomic theorizing has been conceived in the Austrian School. The three models will be expounded in turn, with a review covering in each case the convergence process, the final equilibrium characteristics, and the response to typical exogenous changes (Section One). The second purpose is to analyze the relationships between these models and to expose their theoretical inconsistencies (Section Two). The third purpose is to show that, beyond their differences and contradictions, these models have in common a number of significant general features (Section Three). The fourth and last purpose is to seek to explain why—in contrast with the standard neoclassical paradigm since the classic contribution by Solow (1956) and Swan (1956)—no single basic reference model dominates within the Austrian School (Section Four).
1. THE AUSTRIAN MODELS: A CHRONOLOGICAL PRESENTATION
This presentation of the three basic macroeconomic models aims at elucidating, as briefly as possible, their framework and internal logic. Many secondary features will be left out, so that the length of the paper remains within reasonable limits. In each case the graphical visualization of the model will be used instead of the mathematical formalization, but the latter also exists.2
1.1 Böhm-Bawerk’s Model
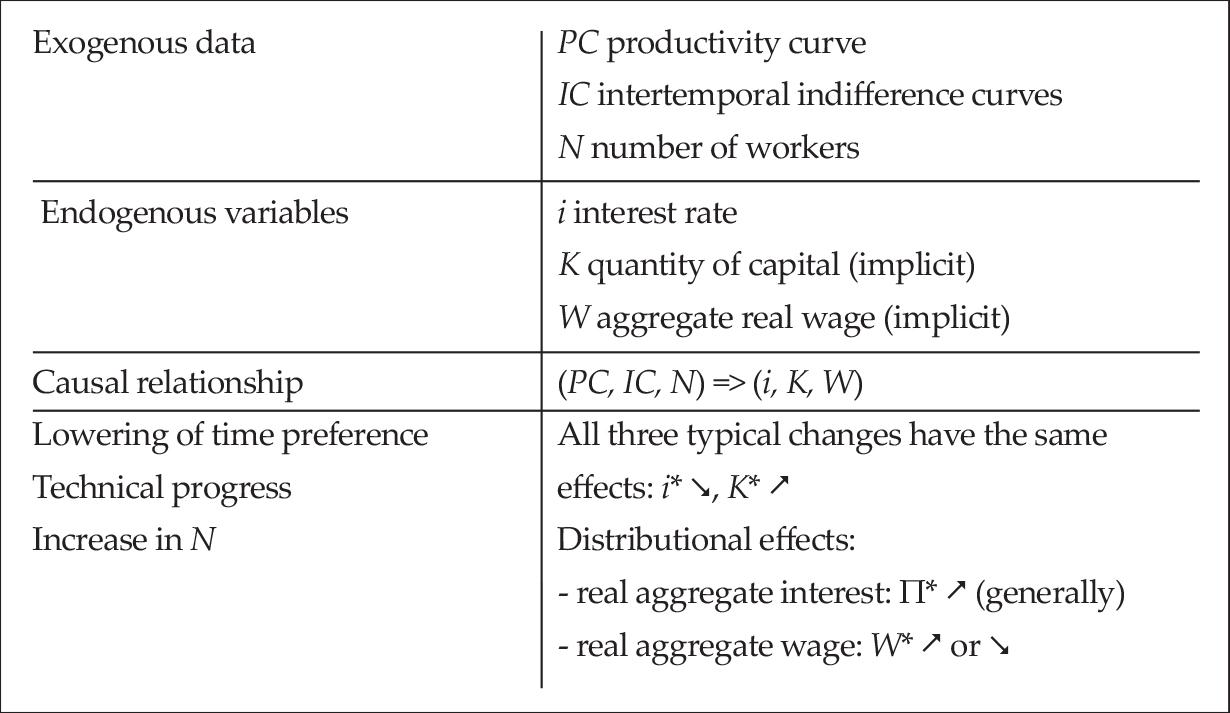
Böhm-Bawerk ([1889] 1959) expounds his model in a chapter titled “The Rate of Interest.” However, his theory is not just a theory of interest and turns out to be a genuine macroeconomic model, in which not only the equilibrium interest rate but also the equilibrium wage and period of production are determined. Böhm-Bawerk was a true pioneer in modern macroeconomic analysis, but his exposé was a bit simplistic in that it was based upon a single numerical example. Wicksell ([1893] 1970) quickly replaced this elementary formulation by a general mathematical presentation using differential equations, and also by a convenient graphical display. Much later, Dorfman (1959) improved upon the Wicksellian graphical version of the model.3 It must nonetheless be noted that this model has not evolved between its original exposition by Böhm-Bawerk and its subsequent representations. It is exactly the same model, and only its form has been refined over time.
The model rests upon two exogenous data, the quantity of capital K and the number of workers N, and upon an exogenous production function f that relates the total period of production T of the economic system to the quantity qc of consumption goods produced per worker and per year. Figure 1 shows this production function qc = f(T) as a concave curve on the top diagram.4 ,5 The function f is increasing, which expresses a central tenet of Böhm-Bawerk’s theory of capital, namely that “roundaboutness” is productive: a “well-chosen” more roundabout method of production produces more consumption goods per period, everything else equal (Böhm-Bawerk [1889] 1959, 82–84). In other words, if T increases, then the annual product per worker qc increases. This increase occurs with diminishing returns that Böhm-Bawerk justifies as an “observation... based on experience” (p. 83).6
Figure 1. Böhm-Bawerk’s model (adapted from Wicksell 1893, p. 122, and Fillieule 2015, p. 309)
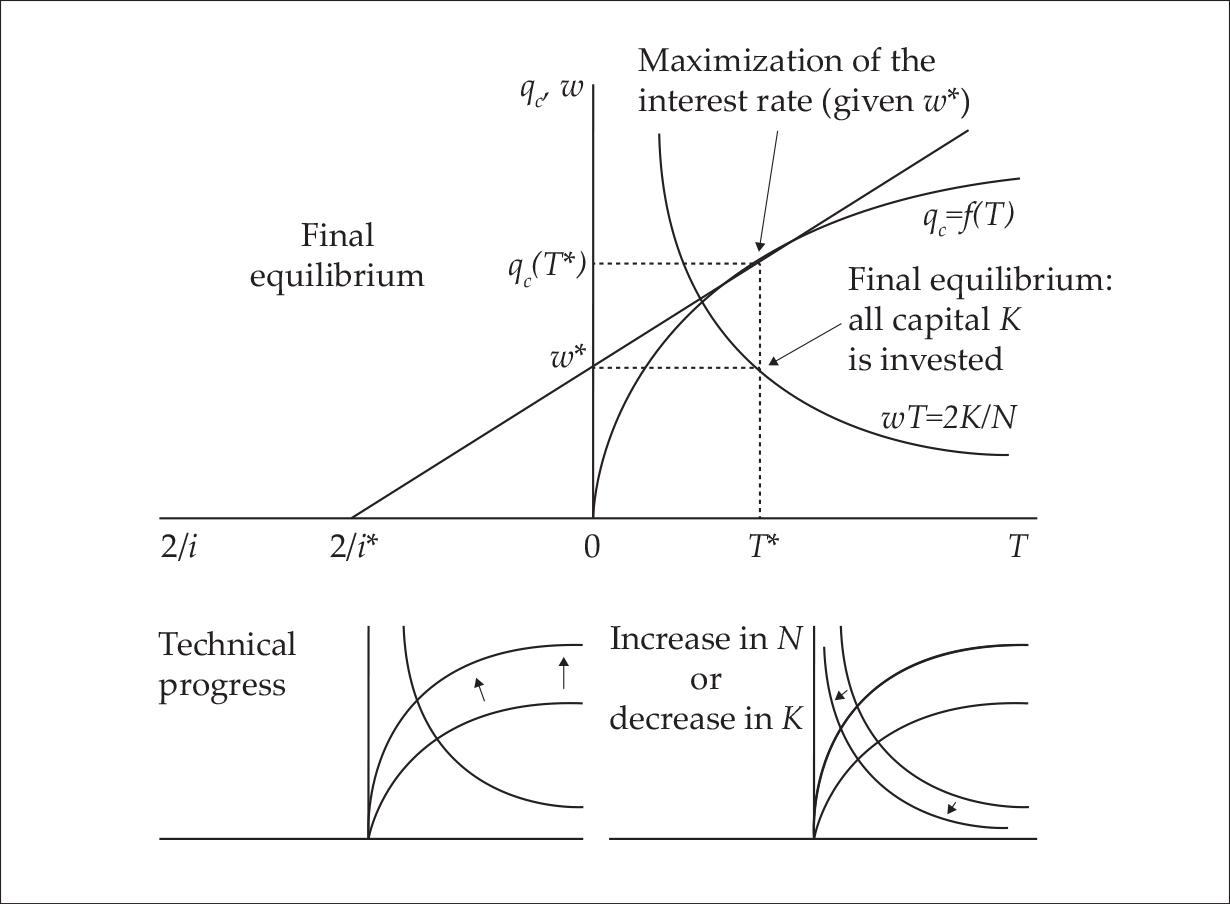
In final equilibrium, two conditions must be fulfilled. The first one is that the whole capital K is invested, no part remaining idle. The second condition is that the capitalists maximize the interest rate (by choosing the appropriate length T for the production process). This optimization condition—maximum interest rate—is visualized on the diagram as the tangency between the production function f and the straight line going through the point (0, w*). If the line going through (0, w*) rotates clockwise, then the ratio 2/i increases (which implies that the interest rate i falls); if it rotates counterclockwise, then no intersection point appears with the production function f and no corresponding economic system exists. The tangency point therefore represents the highest possible level for the interest rate (equivalently, the lowest possible level for 2/i). The graphical relationship illustrated in Figure 1 between the endogenous variables (i, w, T) is the visual translation of the fundamental equation of the model:
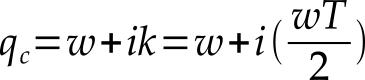
This equation expresses the distribution of the quantity qc of the annual final product (per worker) between the worker (wage w) and the capitalists (interest ik). The quantity of capital k = (wT/2) invested per worker is viewed by Böhm-Bawerk as the subsistence fund required to carry out the process. If all the production processes started at the same date and simultaneously ended T periods later, then the capital—i.e. subsistence fund—required would be k = (wT) (each worker would “subsist” on wage w during T periods). But production is not organized this way. Rather, it is “synchronized” in the sense that, if the length of the production process is T, then there are T processes occurring simultaneously and at different levels of completion.7 The calculation shows that, with a synchronized production, the subsistence fund required falls from k = (wT) to approximately k = (wT/2). The fund is lower because thanks to the synchronization, a part of the subsistence required to sustain a worker is produced by the processes that reach completion while the process in which this worker participates is still under way. The fundamental equation can be written so that the intercept theorem (Thales’ theorem) applies: this theorem is then used to show that the values (2/i), w, T, and qc(T) are necessarily related in the way illustrated in the diagram in Figure 1 (Wicksell 1893).
The convergence process towards equilibrium is carried out through the actions of the capitalists. The latter aim at maximizing the interest rate while competing to invest their funds. Their actions lead the economic system towards an equilibrium characterized by the values (i*, w*, T*) of the three endogenous variables, namely the interest rate, the real annual wage, and the period of production. The convergence process takes place as follows. Initially, an arbitrary wage prevails. Given this initial wage w0 (w0 < w*), the capitalists maximize the interest rate i (in the symmetrical version, the interest rate is given and workers maximize their wage). The maximization of the interest rate is carried out by choosing between the different possible lengths for the structure of production. If the optimal period of production is T0, then the quantity of invested capital is k0 = wT0/2 (per worker) and K0 = NwT0/2 (total). Now, suppose that K0 happens to be below the total available quantity of capital K (exogenous data). The capitalists have some capital left to invest, and they want to invest it to increase their income. So they compete to hire more workers, the demand for labor increases, and the wage therefore rises from w0 to w1. At this higher wage w1, the capitalists once again maximize the interest rate, capital invested once more falls short of the total quantity available, the wage increases again, and so on and so forth. This process keeps on until the wage reaches the equilibrium level w*: at this wage, the maximization of the interest rate determines a period of production T* such that Nw*T*/2 is just equal to the total quantity of capital K (and this configuration is bound to happen because T necessarily goes up when w does, so NwT/2 increases until it is equal to K). At this point, the whole available capital is invested, and the final equilibrium has been reached.
The two lower diagrams of Figure 1 show how the typical changes are visualized. Technical progress is represented as a counterclockwise rotation of the production function. An increase in the supply of labor N is represented as a downward and leftward shift of the (wT) hyperbola. An increase in the quantity of capital K is represented as a shift of this hyperbola in the other direction. It is then possible to analyze the effects of these typical changes on the equilibrium position and, from there, on the distribution of the final product between capitalists and workers.8 This investigation concludes that technical progress is advantageous both to capitalists and to workers, an increase in the quantity of capital favors workers but not necessarily capitalists, and a rise in the number of workers benefits capitalists but harms workers.9 In order for the results to be appropriately interpreted, it should be noted that an individual can be both a worker and a capitalist, even though Böhm-Bawerk seems to implicitly suppose that workers and capitalists are two separate groups of people. Böhm-Bawerk’s model is summarized in Table 1.
Table 1. A summary of Böhm-Bawerk’s model
1.2 Hayek’s Model
In the early 1930’s, Hayek developed the most famous macroeconomic construct of the Austrian School, namely the representation of the structure of production as a triangle displaying the annual nominal consumption and the smaller and smaller annual investment expended into the higher and higher stages (Hayek [1931] 1935). This illustration was inspired by Jevons (1871), but the latter applied it to a single economic process while Hayek used it as a macroeconomic tool to represent the whole economic system. This Hayekian triangle was quite influential and quickly found its way even among authors not members of the Austrian School, such as Abrams (1934, 25–28) and Durbin (1935, 34) who was then a leading economic expert for the British Labour Party.10 It may come as a surprise that this subsection will not at all be devoted to this macroeconomic construct. The first reason is that Hayek did not associate his triangle with a model explaining the determination of the interest rate. This combination was achieved much later by Garrison (1978, 2001) and will be presented in the next subsection. The second reason is that Hayek’s theory of the interest rate (which will be our subject matter here) is incompatible with his triangle, because this theory requires that capital accumulation takes place laterally, while with the triangle capital accumulation takes place longitudinally (see Subsection 2.1).
For these reasons, Hayek’s triangle is left aside for now, and the focus is on his model of the interest rate (Hayek 1936, 1941). Hayek’s model is inspired, not by the theoretical insights elaborated by the Austrian economists since Böhm-Bawerk’s contribution, but rather by the theory of interest developed by the American neoclassical economist Irving Fisher (1930). The main purpose of Hayek with his model is to investigate the question of the determining principle of interest: time preference or productivity? He concludes that productivity is the key factor, but we are not primarily concerned here about this issue. Our focus is on the macroeconomic core of the model, i.e. the convergence towards a macroeconomic equilibrium, the characteristics of this equilibrium, and the study of the effects of typical changes upon the distribution between workers and capitalists.
Figure 2. Hayek’s model (adapted from Hayek 1941, 233). The concave curves are the productivity curves and the dotted curves are the intertemporal indifference curves.
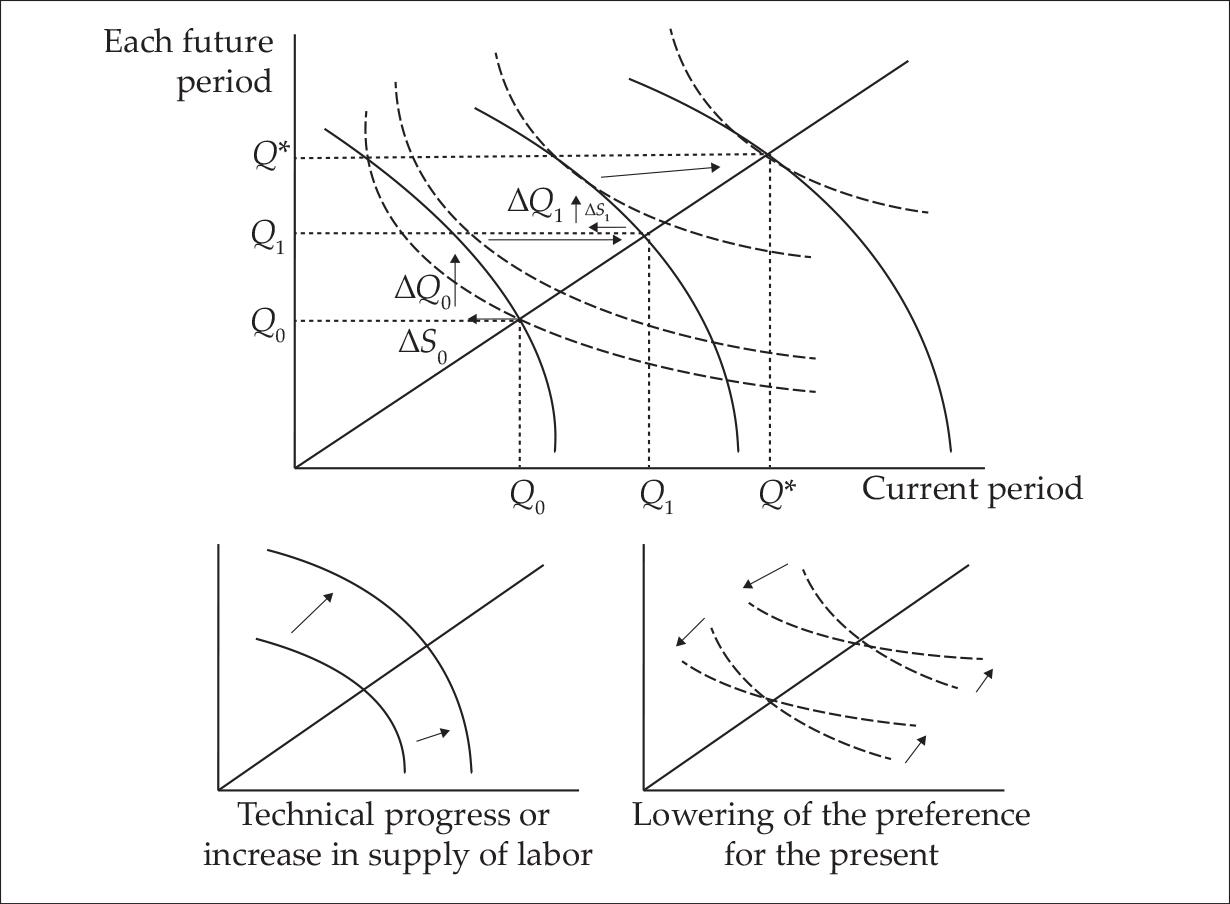
Hayek (1941) presents his model in a figure inspired by Fisher’s classic intertemporal graph (see Figure 2). The difference with Fisher’s graph is that the vertical axis here measures the final output, not just in the next period, but in each and every future period: at the starting point Q0, for instance, the economic system produces the quantity Q0 of consumption goods in the current period (as shown on the horizontal axis: current output) and also Q0 in each future period (as shown on the vertical axis). The concave curve going through Q0 is the productivity curve, showing the additional output that can be obtained in each future period against the corresponding additional amount of present saving. The convex dotted lines are the intertemporal indifference curves. When the economic system is at the starting point Q0, the actors maximize their intertemporal satisfaction—reach the highest possible indifference curve—by saving ΔS0 and getting ΔQ0 additional final product in each future period. In the next period, the system is at the point Q1, and once again the actors maximize their intertemporal satisfaction, this time through saving ΔS1 and getting ΔQ1 additional final product in each future period. Figure 2 only shows the first step of the convergence process (from Q0 to Q1), but this process goes on period after period, until the system finally reaches the equilibrium point Q*. At the point Q*, the productivity curve and indifference curve are tangent to each other on the 45-degree line, so that the actors cannot improve their intertemporal satisfaction (i.e. cannot get to a higher indifference curve), either through saving or through dissaving. The economic system has therefore reached a state of final equilibrium: marginal productivity and marginal time preference are equal, and their identical value is the equilibrium interest rate. In other words, the equilibrium interest rate is equal to the common slope of the productivity curve and the indifference curve on the 45-degree line.
Hayek first analyzes the case of a linear productivity curve (1941, 222), and then the more general case of a concave productivity curve (1941, 233). Only the latter, exhibiting the diminishing returns on capital accumulation, is represented here.11 The bottom diagrams of Figure 2 display the typical changes. The bottom-left diagram illustrates both a technical progress and an increase in the supply of workers, through an upward shift and a rotation clockwise of the productivity curve. The bottom-right one illustrates a lowering of the preference for the present, through a rotation counter-clockwise of the pattern of indifference curves. The effects of these changes upon the distribution of the final output between capitalists and workers, depend on the hypothesis made about the pattern of intertemporal indifference curves. There are two main possibilities: as the economic system becomes more productive and wealthier (climbing the 45-degree line), people can become more present-oriented, or they can become less present-oriented. Correspondingly, the marginal rate of time preference can respectively increase or decrease as wealth grows. Graphically, these two cases are illustrated by the indifference curves becoming respectively steeper or flatter on the 45-degree line (see Figure 3). Under the assumption of a concave productivity curve, the two configurations are compatible with the existence of an equilibrium.12 However, the pattern with an increasing time preference is quite unlikely, since it implies that as people become wealthier, they are more and more eager to consume their marginal net income rather than saving and investing it. It is more plausible that, when people become wealthier, they also become more, not less, prone to save an extra unit of present good in order to get additional units in the future (see the discussion in Block, Barnett and Salerno 2006). This pattern—a decrease of time preference with wealth—is illustrated in the right diagram of Figure 3, and the consequences of the typical changes in the case when this pattern prevails are summarized in Table 2.
Figure 3. Two patterns of time preference in Hayek’s model
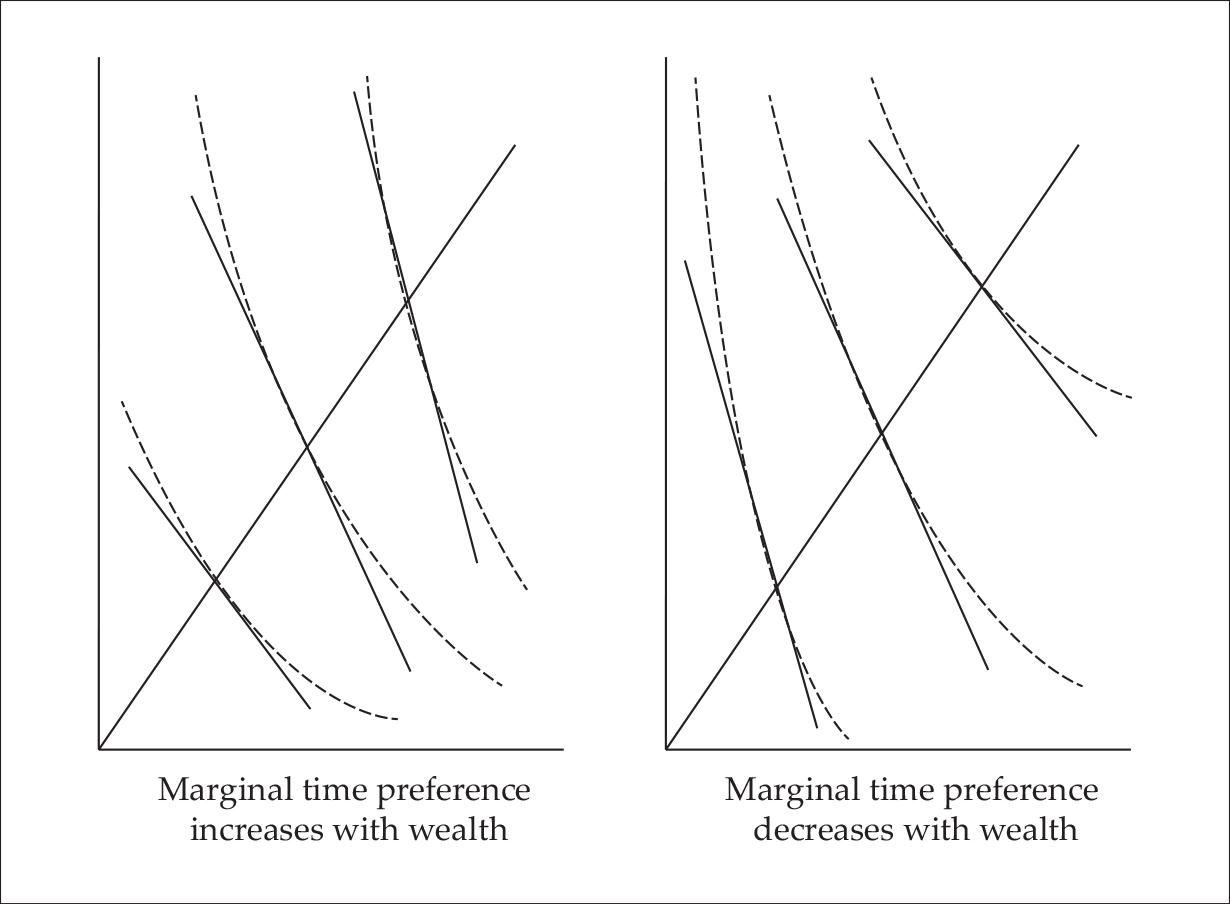
Table 2. A summary of Hayek’s model (the effects of the typical changes are those that occur under the assumptions of a concave productivity curve and of a marginal time preference that decreases with wealth)
1.3 Garrison’s Model
The models of Böhm-Bawerk and of Hayek rest upon an optimization process (graphically: a tangency between curves). Garrison’s model, on the other hand, rests upon the equalization between a supply and a demand (graphically: a point of intersection between two curves). Here, equilibrium is determined on a generalized loanable funds market.13 The intersection of the supply of and demand for loanable funds displays the equilibrium values of the interest rate and of the gross investment spending. These values are then used to determine the shape of a Hayekian structure of production, through the use of the production possibilities frontier (PPF) of the economic system (see Figure 4). This frontier indicates the “fundamental trade-off between consumer goods and capital goods” (Garrison 2001, 41): a greater investment during the current period requires a lower consumption, and a lower investment allows for a greater current consumption. For an equilibrium amount of investment Ie as determined on the loanable funds market (bottom-right quadrant), the PPF indicates the corresponding equilibrium amount of final consumption Ce, and from there on the Hayekian structure of production is itself determined (top-left quadrant).
Figure 4. Garrison’s model (adapted from Garrison 2001, 50)
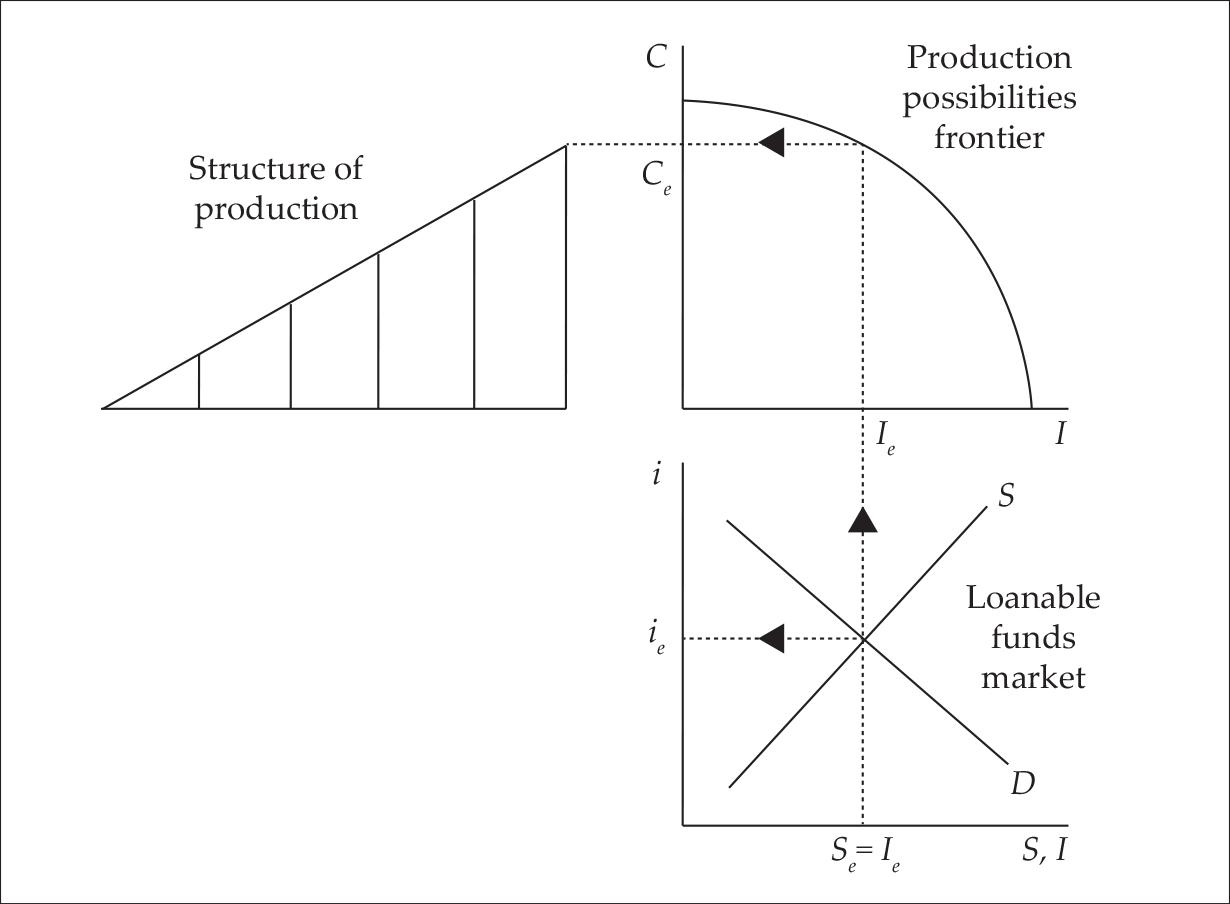
The typical changes analyzed by Garrison are (i) a technical progress and (ii) a lowering of time preference (there is no mention in his presentation of a change in the aggregate supply of labor). Let us begin with technical progress. If this progress “affects all stages of production directly and proportionally,” then “Investment, output, income, consumption, and saving would all rise together without putting pressure one way or the other on the rate of interest” (2001, 58). If, on the other hand, the technical improvement “is usable only in one or a few stages,” then the interest rate is impacted: first, the demand for loanable funds increases and the interest rate rises, as entrepreneurs “seek to take advantage of [the] new technology”; then, as incomes increase due to the enlarged investment, the supply of loanable funds also increases, and the interest rate falls; equilibrium aggregate investment Ie necessarily rises, but the resulting effect on the equilibrium interest rate ie is indeterminate since the effects of a higher demand for and a higher supply of loanable funds balance one another. Simultaneously, the PPF shifts outward since the economic system has become more productive, so that the amount of final consumption and the period of production also rise. In the case of a lowering of time preference: the supply of loanable funds shifts to the right, since people are willing to lend and invest more, but the demand does not move. As a consequence, the equilibrium interest rate diminishes, equilibrium investment increases, consumption falls, and the structure of production becomes more roundabout.14 Garrison’s model is summarized in Table 3.
Table 3. A summary of Garrison’s model

2. VIENNA, WE HAVE A PROBLEM
After this review of the Austrian models, the first and most obvious remark is that they are inconsistent with each other. In the case of the implementation of technical progress, for instance, Böhm-Bawerk’s model concludes that the interest rate will rise, while according to Hayek’s model it will rise first and then fall more than it has risen (under the assumption that time preference diminishes with wealth), and in Garrison’s model it can either rise or fall. In the case of a lowering of the preference for the present, all the models conclude that the interest rate falls and that investment necessarily increases. However, even when the conclusions converge they are deduced from incompatible premises, and this is the deeper problem that will be investigated hereafter. In order to carry out the comparison between these models, we are going to distinguish between the “productivity” models of Böhm-Bawerk and of Hayek on the one hand, and the “demand and supply” model of Garrison on the other. The comparative analysis will be carried out first between the “productivity” models, and then across the two kinds of models.
2.1 The “Productivity” Models
In both Böhm-Bawerk’s and Hayek’s models, productivity plays a key role and the convergence towards equilibrium takes place through a step-by-step optimization process, but there are significant differences between them. The first and main one pertains to intertemporal choice. In the two models, the economic agents make intertemporal decisions, but not at all of the same kind. In fact, while Hayek’s model is built upon a genuine intertemporal choice, Böhm-Bawerk’s rests upon what can be called a “pseudo” intertemporal choice. The actors in Hayek’s model face a trade-off between present and future consumption. If they want to consume more now, they must decumulate capital, and the less capitalistic structure will provide a smaller output and consumption in the future. Conversely, if they sacrifice a part of their present consumption and invest this net saving, then capital is accumulated, and the more capitalistic structure will provide a larger output and consumption in the future. There is of course nothing surprising or unusual in this kind of very basic intertemporal arbitrage. However, when we turn to what Böhm-Bawerk calls the “exchange” of present against future goods by capitalists, we realize that the phenomenon he is talking about is completely different.15 Here, the capitalists “exchange” present goods (present wages) against the goods that will be produced in the future with the help of the hired labor. In these exchanges, the capitalists invest the same amount at the beginning of a period (the wage), and they can get, over the period, different levels of interest rate according to the length T of the structure of production. It so happens, in the framework of the model, that there is a period of production that brings the highest interest rate (and also interest), and they choose this period. The crucial point is that the capitalists choose the highest interest that they can get at the end of each period, while their investment at the beginning of this period is fixed. This means that they do not choose between present and future goods, but rather between future goods available at the same moment (at the end of the period): at this moment, the capitalists can get more or can get less, and choose more over less. This choice cannot appropriately be considered as an intertemporal choice because it is made between options available at the same moment in time. Whether the period of production is longer or shorter does not require a greater or smaller sacrifice from the capitalist. There is no trade-off between present and future consumption. While the exchange in Hayek’s model is truly intertemporal, in Böhm-Bawerk’s it only appears, but is not, intertemporal.
The second significant difference between the two models has to do with the roundaboutness of the production process. The period of production is a pillar of the Austrian theory of capital, according to which capital accumulation takes place through a lengthening of the structure of production. Böhm-Bawerk’s model explicitly takes this length T into account as an endogenous variable. The period of production thus plays a key role in his formalization. Hayek (1941, 60) accepts the “roundaboutness” theory but maintains that it is not applicable in the framework of his model. The reason is that in his model “there is only one possible period of investment” (1941, 221), and as a consequence there cannot be any change in the duration of the period of production: capital accumulation takes place laterally, through the addition of similar processes of identical length, not longitudinally. His model indeed requires that, when an extra saving is invested, the increase in the production of consumption goods occurs in the very next period. Now, when the period of production lengthens, the reorganization of the structure extends over several periods, which means that a number of periods elapses before the eventual increase in the production of consumption goods. But such a waiting cannot happen in the framework of the model, which requires that the production of consumption goods increases in the period immediately following the period when the net saving is invested. Hayek’s model therefore does not integrate the phenomenon of roundaboutness that is the fundamental law of the Austrian theory of capital.16 To sum up, when compared to Böhm-Bawerk’s model, Hayek’s one offers a much more appropriate formalization of intertemporal choice, but uses a theory of capital accumulation that is not the core theory of the Austrian School.
2.2 Across “Productivity” and “Demand and Supply”
The “productivity” models are well suited for the study of changes that affect the real output, such as technical progress and an increase in the supply of labor: suffices to move the productivity curve and investigate the ensuing convergence process. The “supply and demand” model of Garrison, on the other hand, is especially appropriate for the study of lending and borrowing. Two questions now deserve to be answered. First, how does this “supply and demand” model address the issue of productivity? And second, are the “productivity” models able to integrate the phenomenon of lending and borrowing?
Can productivity be taken into account in the “demand and supply” model? Productivity has to do with quantities of goods, i.e. with real values. In Garrison’s model, there is an element that shows the real final output, namely the production possibilities frontier (PPF). Technical progress simultaneously affects the PPF and the loanable funds market. The PPF moves upwards, since for any level of investment I, the real final output Cr is now larger. In parallel, the supply and demand curves increase, simultaneously if technical progress is implemented all along the structure of production, and sequentially if it is implemented at one stage only (see Subsection 1.3 above). This “supply and demand” model can therefore analyze the productivity effects, even though its theory is in this case more convoluted than those offered by the “productivity” models.
This is the place to say a few words about the comparison between the Garrisonian PPF and the Hayekian productivity curve. These two curves bear a superficial resemblance, as they are both concave curves that relate consumption to investment. However, the two constructs are very different from each other. The Hayekian productivity curve is an intertemporal construct that shows how future consumption will change following a current net saving or dis-saving. This productivity curve therefore shows how a current net saving (for instance) turns into an increase in future consumption. Garrison’s PPF, on the other hand, is an instantaneous construct that shows how a current net saving implies a decrease in current consumption. Another difference is that the Hayekian productivity curve is a barrier that the economic system cannot cross, while the Garrisonian PPF is a boundary that can be crossed: the economic system can move beyond it. Garrison (2001, 70) defines the PPF as “sustainable combinations of consumption and investment,” so the economic system can indeed produce an amount that goes beyond the frontier if part of the capital is consumed.
The “supply and demand” model can take productivity into account, but can the “productivity” models integrate the phenomenon of lending and borrowing? The answer, in our opinion, is no. Hayek’s and Böhm-Bawerk’s models are exclusively based upon productivity. They have no place for a loanable funds market in which the economic agents supply or demand various amounts of present goods according to the level of the interest rate. Hayek (1941) never mentions loans in the two chapters of the book in which he develops his model. Böhm-Bawerk ([1889] 1959, 369) takes consumer loans into account, but not in his basic model, since the latter only features the wage and productivity of capital. He analyzes the demand for consumer loans separately, as an additional and specific force that impacts the interest rate and the structure of production: the economic agents who ask for consumer loans compete with workers to get a part of the subsistence fund; the more intense the demand for consumer credit, the higher the interest rate, and the shorter the structure.17
Leaving aside consumer loans and focusing on the more relevant phenomenon of productive loans, a follow-up question arises: is it a serious defect for these “productivity” models that they do not integrate loans to producers? The answer depends in turn on the answer to another question: how significant is the role of loans to producers in a basic macroeconomic model? In the context of such a study, investors do not face any uncertainty, and have thus no reason to prefer less risky loans to more risky equity. Furthermore, there is no money creation by banks building additional credit (loanable funds) upon fractional reserves. It appears, therefore, that productive loans would play a secondary role in the study of the determination of investment and the interest rate. The fact that the “productivity” models cannot explicitly take these loans into account is therefore not at all a critical flaw. Furthermore, a developed economic system can be conceived without any loans, but not without any productivity of capital, so that the latter is more important from a theoretical viewpoint.18
In conclusion, there are bridges between a “demand and supply” model such as Garrison’s and the phenomenon of productivity. The relationship between the “productivity” models and the phenomenon of productive lending and borrowing is more problematic, and has not been investigated either by Böhm-Bawerk or by Hayek in the framework of their “productivity” models.
3. SOME COMMON FEATURES OF THE AUSTRIAN MODELS
Even though the three models widely diverge in their specifics, at a more general level they share a number of significant characteristics.
First, they all implicitly or explicitly accept the validity and relevance of a “macro” approach in the realm of economic analysis. The idea of an “Austrian macroeconomics” may at first sight seem problematic and even paradoxical, on account of the importance that the economists of the Austrian School have attached to subjectivism and individual action since the seminal contribution by Menger ([1871] 1976). Now, as much as the proof of the pudding is in the eating, the proof of an Austrian macroeconomics is in the models presented above. Horwitz (2000, 1) writes that “In the eyes of many economists, Austrians are seen as rejecting the whole concept of macroeconomics in favor of a focus on microeconomic phenomena such as price coordination and entrepreneurship.” He adds that “there is an Austrian macroeconomics that is alive and well” (2000, 2), pointing to the study of topics such as money, banking, and the business cycle. This paper shows that Austrian macroeconomics is not limited to the theories of monetary disequilibrium and of cyclical fluctuations. It also covers much more elementary topics such as the determination of the static equilibrium interest rate and distribution between capitalists and workers. Like Horwitz, Hülsmann (2012) recognizes the existence of an Austrian macroeconomics. He notes that before Garrison’s first contribution (Garrison 1978), “the very expression Austrian macroeconomics was considered an oxymoron” (2012, 46) because the word macroeconomics was associated “with positivistic and mercantilist ideas,” ideas to which the Austrians were—and still are—strongly opposed. However, it can be argued that the Austrian tradition in macroeconomics was not born in the 1970s, but goes way back to the end of the nineteenth century.
The second common feature of these Austrian models is that they all have, in one way or another, a subjectivist foundation in human action. In Böhm-Bawerk’s model, the convergence process is driven by the capitalists aiming at maximizing the interest rate, and also competing with each other to invest their whole capital. Hayek’s model is formalized around the intertemporal choice of a Robinson Crusoe or a collectivist dictator. Garrison’s model is based upon a generalized loanable funds market in which the individual actors interact. Since the appearance in the 1930s of a macroeconomics severed from any micro-foundations (Frisch 1933), the Austrian scholars have ceaselessly criticized this kind of approach. Hayek was one of the earliest opponents of this search for relationships between aggregate statistical constructs,19 but his attack should not be understood as a criticism against any and all kind of macroeconomic investigation. The Austrian models do not suffer from the defects of the purely holistic macroeconomics that he strongly condemns. In the distinction elaborated by Lachmann (1973) between “formalism” and “subjectivism,” these models clearly belong to the latter category. Lachmann defines “formalism”—an approach with which he disagrees—as “a style of thought according to which abstract entities are treated as though they were real.” He then defines “subjectivism” as “the postulate that all economic and social phenomena have to be made intelligible by explaining them in terms of human choices and decisions” (1973, 9–10). The Austrian macroeconomic models indeed rest upon the subjectivist approach, in line with the Mengerian tradition of methodological individualism.
Third, all the models use very similar simplifications in order to make the analysis of the economic system manageable. These simplifications are too numerous to be listed exhaustively, but here are some of the most significant. The economic system produces a homogenous consumption good or basket. The capital goods, on the other hand, can be different from the consumption good, and to this extent these models are not as simple as the standard neoclassical model of Solow and Swan, in which there is only one good used both as a capital and as a consumption good. There are two kinds of factors of production, namely labor and capital goods (in the Böhm-Bawerkian sense of produced factors of production). In the more general case, there are three kinds of factors, labor, capital goods and land. If land is taken into account, then the corresponding (unproduced) natural resources are not exhaustible: if there were an exhaustible resource, then a static equilibrium could not occur because the quantity of one of the productive inputs would diminish over time. When the effect of technical progress is analyzed, the discovery of more efficient techniques of production is free, and these more advanced methods increase final production as soon as they are discovered and implemented.20 The functioning of the price system that reallocates the factors of production where they are the most useful is taken for granted, and quickly adjusts the structure of production after an exogenous shock. Finally, these models eliminate uncertainty, and with it the entrepreneurial function. The absence of uncertainty gives them a “mechanistic” appearance that is discordant with the work in the Austrian paradigm that is more focused on the way the market process allows the agents to cope with radical ignorance.21 This mechanistic aspect, however, seems to be the price to pay for the high degree of simplification required in order to cope with an economic system as a whole.
On the theoretical side also, these models bear an undeniable resemblance. As far as production is concerned, it can only grow if the quantities of factors increase or if better techniques are implemented. The increase in the quantities of factors can be either exogenous in the case of the original factors labor and land, or endogenous (through saving) in the case of capital goods. In all these models, the crucial theoretical problem that has to be solved is the problem of the determination of the interest rate. In fact, for two of the three models (Böhm-Bawerk’s and Hayek’s), the essential reason they were developed was to get a theory of the forces that lead to the determination of the level of the interest rate. In the case of Hayek, the problem was to weigh the relative influence of productivity and of time preference on the height of the interest rate. Another major theoretical similarity is the kind of shocks whose effects upon equilibrium and distribution can be analyzed, namely a change of time preference (capital accumulation or dissipation), technical progress, and a change in the supply of labor. A last theoretical common point between the models is the use of the Austrian structure of production and of the related Böhm-Bawerkian theory of roundaboutness. The only model that does not resort to either of these two elements is Hayek’s model, for reasons indicated above (see Subsection 2.1). It is surprising that Hayek’s model is the one that does not make use of the most famous construct in Austrian macroeconomics, namely the Hayekian triangle developed by Hayek himself ([1931] 1935).
Finally, from an epistemological viewpoint, the three Austrian models all exemplify the same kind of endeavor. They are not intended to be tested against empirical observations. They are not meant to be calibrated to match historical macroeconomic data in order to determine the value of their parameters.22 Rather, they are conceived as intelligibility models that aim at clarifying some of the most basic economic questions in a very simplified setting. This clarification rests upon the logic of action, and has nothing to do with the empirical corroboration of hypothetical laws. These models therefore follow an epistemology that is not the one used in the experimental sciences.23
For all these reasons, in spite of their divergences, the three Austrian models are part of the same family. They can be considered as declinations or exemplars of a common approach to basic macroeconomics, illustrating the search for simple frameworks that illuminate the determination of the interest rate and the distribution of the net output. All these attempts agree on the purpose of a straightforward and relevant macroeconomic model in terms of equilibrium analysis and response to typical shocks.
4. WHY NO SINGLE MODEL DOMINATES
Up to this point, it has been established that the Austrian macroeconomic models are contradictory in their premises and conclusions, but bear a family resemblance. The question remains as to why none of them has managed, at least until now, to dominate the scene within the Austrian School, and by “dominate” we mean: being generally accepted within the School as a sound theoretical foundation.
Böhm-Bawerk’s model was published in 1889, and was mathematically formalized a few years later by Wicksell ([1893] 1970). There is, however, no trace of this model in Wieser’s treatise ([1914] 1927), nor in Strigl’s main book on capital ([1934] 2000). The model was revived by Dorfman (1959), and the last specific reference to it by a major Austrian economist is found, to the best of our knowledge, in Kirzner (1966).24 In the meantime, the two main Austrian economists of the twentieth century, namely Mises and Hayek, had both aimed severe criticisms at Böhm-Bawerk’s approach of the theory of interest. Their criticisms are not consistent with each other, though, and furthermore do not rest upon a detailed examination of the model itself. Rather, they target some of the most general features of Böhm-Bawerk’s approach. Hayek (1941) criticizes the simplistic assumptions made by Böhm-Bawerk when he treats the quantity of capital and the period of production as purely technical data.25 Mises is extremely severe vis-à-vis the Böhm-Bawerkian concept of “average period of production,” which he labels an “empty concept.”26 He also totally rejects the productivity theory of interest that forms the core of Böhm-Bawerk’s model. In this regard, the opinions of Mises and of Hayek diverge: Hayek considers Böhm-Bawerk’s criticism of earlier productivity theories as “mistaken,”27 while Mises lauds how “brilliantly” Böhm-Bawerk refuted these first productivity theories.28 So they both point out what they believe to be insurmountable flaws in Böhm-Bawerk’s theory. The latter’s model, therefore, could not be accepted by the followers either of Mises or of Hayek, which pretty much means that it could not be accepted by anyone in the Austrian School from the mid-twentieth century on.
In the 1970s, Faber (1979) developed a “neo-Austrian” approach to the theory of capital. After an in-depth analysis and criticism of Böhm-Bawerk’s model, Faber makes use of a mathematical model of the economic equilibrium elaborated by von Neumann (1945–46). This model rejects the concept of an average period of production, but it can be infused nonetheless with the Böhm-Bawerkian theory of roundaboutness. Faber is able, with his neo-Austrian version of von Neumann’s model, to investigate the cases of a two-period two-sector economy, and then of a multi-period (with a finite horizon) economy.29
Hayek’s model has recently been brought to light by Molavi Vasséi (2015) and Fillieule (2017). White (2007) also devoted a few paragraphs to it in his “Introduction” to the new edition of Hayek (1941). There are a number of reasons why this model has not been used to build a cumulative tradition. The first one is that Hayek’s book failed to have a significant following in the Austrian School, in the sense that nobody tried to develop capital theory along the lines first set out in this book. Furthermore, the model does not deal with the core topic of the 1941 book, namely capital theory. An off-topic model in an idiosyncratic book had little chance to make an impression.30 A second reason is that the model was not conceived, and also not really recognized, as a macroeconomic model. In his ([1936] 2015) paper, Hayek insists upon the way his model formalizes time preference, and claims that the concept of “constant tastes” failed to be correctly understood by Böhm-Bawerk and by Schumpeter. Hayek ([1936] 2015, 36) then explains that “we... have to represent constant tastes by declaring the indifference map of the individual (or the indifference maps of all the individuals) to be the same at every moment.” His model indeed solves the problem of formalizing “constant tastes” as a pattern of intertemporal indifference curves that remains the same at the successive periods. But as a result of this presentation, the much wider range of the model may have been neglected. There were also probably more technical reasons, such as the hypothesis of a constant marginal productivity (which deprives the model of much of its appeal, since it restricts the acceptable kind of time preference pattern to the implausible case of a marginal time preference that increases with wealth), and such as the fact that Hayek did not systematically try to investigate the effects of changes in time preference, technology, and supply of labor. A major reason for the neglect of this model is that in the United States, where the Austrian School experienced a renaissance in the second half of the twentieth century, the scholars adopted the Fetter-Mises subjectivist theory of interest instead of a productivity theory. The time preference theory of interest was endorsed by Rothbard ([1962] 2009), Garrison (1979), Kirzner (1993), and other authors (see Pellengahr 1996). Hayek (1941), on the other hand, very explicitly chose the productivity explanation of interest, even though he thought that time preference could also play a (minor) role in the determination of interest.31 As a result, his model—interpreted by Hayek as a validation of the productivity theory of interest—was largely overlooked.
Garrison’s model (2001) attracted a lot of attention within the Austrian School as soon as it was published. The reason is that this author had provided for more than two decades some of the most important macroeconomic work of the school (see for instance Garrison 1984). The book (not just the model) was received with great expectations by the Austrian scholars, but the reviews that were published in the two major Austrian journals were not entirely positive. In the Review of Austrian Economics, Oprea and Wagner (2003) criticized Garrison’s book for being dated, reviving discussions from the 1960s, and for not taking into account the more recent mainstream macroeconomic paradigms. The Quarterly Journal of Austrian Economics devoted a whole issue to the analysis and commentary of the book (Thornton 2001). While more positive in tone than Oprea and Wagner’s review, a number of criticisms were raised. The comments about the comparison drawn by Garrison between his “capital-based macroeconomics” and the macroeconomics of Keynes and Friedman do not concern us in this paper, and neither do the comments about the theory of the business cycle. The graphical construct is the focus here, and it was criticized by Hülsmann and by Salerno. Hülsmann (2001, 40) notes two inconsistencies in the diagrams displayed by Garrison (see Figure 4 above). First, there is a discrepancy between the nature of the variables in the top part of the diagram, namely between the real consumption on the vertical axis of the PPF and the nominal consumption on the vertical side of the Hayekian triangle. Second, there is a temporal discrepancy between the two horizontal axes, the bottom horizontal axis showing the current investment that will produce the future capital goods, and the top horizontal axis showing these future capital goods on the PPF. Salerno (2001) criticizes another aspect of the model, this time pertaining to the theory of growth. Garrison (2001, 54) claims that a “secular growth” can occur “without having been provoked by policy or by technological advance or by a change in intertemporal preferences.” This secular growth is simply the result of “the ongoing gross investment,” which “is sufficient for both capital maintenance and capital accumulation.” Salerno points out that the Austrian theory asserts, rather, that the growth brought by a net investment ends up in a stationary equilibrium and cannot lead to an indefinite growth.32 So, even though Garrison’s diagrammatic exposition of Austrian macroeconomics was generally praised as a pedagogical tool (and still is33 ), some of the reviewers were skeptical about parts of the theoretical underpinnings of the model.
CONCLUSION
This paper has attempted to tell the little-known story of the basic Austrian macroeconomic models, models spanning from the end of the nineteenth century to the beginning of the twenty-first. After a presentation of each model, a detailed account of the differences between them has been provided. The main results of this investigation can be summarized as follows. (i) There exists an Austrian macroeconomics, even at a quite elementary level that does not take uncertainty and monetary disturbances into account. (ii) This macroeconomics is embodied in formal models that have been presented graphically as well as mathematically. (iii) These models are not consistent with each other. (iv) The inconsistencies between them are mainly due to disagreements on the theory of the interest rate. (v) Beyond these theoretical contradictions, these models all try to solve the same kind of problems by using of the same (actionist) methodology. (vi) The continuing search for a basic macroeconomic model, from the birth of the Austrian school until today, shows the importance and relevance of this topic from a theoretical viewpoint. (vii) Nevertheless, very few discussions, if any, have taken place in the history of this school on the relative merits of the different models. From a history of thought perspective, this study shows that in macroeconomics just as in other areas (banking, for instance), the Austrian School is not monolithic but has been traversed by deep tensions, some of them still unresolved.
- 1Hülsmann (2010) has developed a macroeconomic model that integrates Rothbard’s model of determination of the pure interest rate and the Hayekian structure of production, but it is still a working paper and can therefore not yet be considered as an “official” contender. Fillieule (2005) has expounded a graphical model illustrating the interrelations between various aspects of the economic system, but it lacks a very important element, namely a theory of interest.
- 2Wicksell ([1893] 1970) developed both the mathematical and the graphical versions of Böhm-Bawerk’s model, Molavi Vasséi (2015) developed the first mathematical formalization of Hayek’s model, and Cachanosky and Padilla (2016) the first mathematical formalization of Garrison’s model.
- 3See Fillieule (2015) for a recent and comprehensive graphical account of the model.
- 4Lower cases are used for individual variables, and upper cases for aggregate variables.
- 5Two differences between the production functions respectively used in Böhm-Bawerk’s model and in the well-known Solow-Swan model can be briefly highlighted. First, the Böhm-Bawerkian macroeconomic function of production determines the annual quantity Qc of consumption goods produced, not the total quantity of consumption and capital goods. Second, the argument of this Böhm-Bawerkian function is the period of production T of the economic system, not the quantity of capital K (for a given quantity of labor N).
- 6These diminishing returns should rather be explained by the fact that there is a fixed factor, namely labor.
- 7If a process lasts for three periods, for instance, then a “synchronized” system comprises three simultaneous processes: at the beginning of each period, one process just begins (and will be completed three periods later), another process is half-way (and will be completed two periods later), and the third process nears completion (and will be over at the end of the current period). Thanks to this synchronization, the final product is delivered in each period, instead of waiting for the many periods required to complete a single process.
- 8Böhm-Bawerk (1959 [1889]) thoroughly analyzes the effects of the typical changes on the level of the interest rate, but only cursorily notes the effects on the level of wages (for instance on p. 378).
- 9Böhm-Bawerk does not take into account here the increasing returns due to the intensification of the division of labor that follows a multiplication of workers. He never mentions these increasing returns in the chapter. He only refers, in the penultimate footnote (1959 [1889], 461, footnote 52), to the diminishing returns on labor brought about by an increasing population.
- 10The author wishes to thank an anonymous referee for these references.
- 11At this point, we skip the quite important but a bit technical discussion by Hayek of the shape of this productivity curve. When the productivity curve is linear, the equilibrium interest rate is necessarily equal to the (constant) marginal productivity, and therefore does not depend on time preferences. Hayek argues that the productivity curve is linear or almost linear, and concludes that the level of the equilibrium interest rate is determined by productivity, not by time preferences.
- 12In Hayek’s first model, i.e. with a linear productivity curve, then the existence of an equilibrium necessitates an increase of time preference with wealth (Molavi Vasséi 2015).
- 13This market is generalized in the sense that it includes, not only business lending and borrowing in the strict sense, but also “retained earnings and saving in the form of the purchasing of equity shares” (Garrison 2001, 36).
- 14The lengthening of the structure increases the productivity of labor and will eventually cause an outward movement of the PPF, but Garrison does not illustrate this effect.
- 15Böhm-Bawerk uses the word “exchange” many times in his chapter on “The Rate of Interest,” for instance in the very first sentence that reads: “The exchange of present goods for future goods, which constitutes the source of the phenomenon of interest, is merely one special case under the rubric of the exchange of goods in general” ([1889] 1959, 347).
- 16This impossibility to integrate the phenomenon of roundaboutness is (in our opinion) the reason why Hayek did not try to combine his theory of the interest rate of The Pure Theory of Capital (1941) with his famous “triangle” of Prices and Production ([1931] 1935). When the economic system is depicted as a triangle, capital accumulation takes place through a lengthening of the overall period of production: the triangle becomes thinner and longer. This “longitudinal” or “vertical” accumulation of capital is incompatible with Hayek’s theory of the interest rate.
- 17In the graphical representation of Böhm-Bawerk’s model (see Figure 1), the effects of the emergence of a demand for consumer loans can be visualized as a downward movement of the hyperbola wT = 2K/N, since this demand reduces the amount of capital K available for productive purposes.
- 18In the context of his discussion of the tendency towards an equilibrium, Hayek (1941, 266) writes:
We might conceive a society where the lending of money (at least at interest) was prohibited and where nevertheless, so long as the possibility of spreading investments by means of partnerships, joint-stock participation, etc., existed, the rate of return on investment would be uniform throughout the system. The rate of return on investment as determined by the price relationships between capital goods and consumers’ goods is thus prior to, and in principle independent of, the interest on money loans, although, of course, where money loans are possible, the rate of interest on these money loans will tend to correspond to the rate of return on other investments (our emphasis). Hayek does not clarify what he means by the rate of return on investment being “prior to” the interest on money loans, but he is likely talking of a historical and a theoretical priority. Decades before, Fetter ([1914] 1977, 234) argued that “capitalization” (interest on investment) is both historically and logically antecedent to “contract interest” (interest on loans).< - 19“In fact, neither aggregates nor averages do act upon another, and it will never be possible to establish necessary connections of cause and effect between them as we can between individual phenomena, individual prices, etc.” (Hayek [1931] 1935, 4–5). He expressed the very same thought in his last book, defining what he calls “macro-economics” as the search for “causal connections between hypothetically measurable entities or statistical aggregates,” and stating that it is a “delusion that macro-economics [in this sense] is both viable and useful” (Hayek 1988, 98).
- 20It would be more realistic to suppose that there is a delay between the implementation of new techniques and the eventual increase in the production of consumer goods. If the progress takes place at a stage far away from final consumption (for instance an improvement in the methods of extraction of deposits), then it could take several years before the increase in the final output occurs.
- 21As Lachmann ([1991] 1994, 278) puts it, “In its essence Austrian economics may be said to provide a voluntaristic theory of action, not a mechanistic one. Austrians cannot but reject a conceptual scheme, such as the neoclassical, for which man is not a bearer of active thought but a mere bundle of ‘dispositions’ in the form of a ‘comprehensive preference field.’”
- 22We are not claiming that it would be impossible to relate in one way or another these models to macroeconomic data, but it certainly has never been attempted and was not the reason why they were developed in the first place.
- 23Hayek (1952) and Mises (1962) offer classic statements, from an Austrian perspective, of the epistemological specificity of the social sciences vis-à-vis the natural sciences.
- 24Blaug ([1962] 1978) offers a detailed presentation of the model in the chapter devoted to the Austrian theory of capital and interest.
- 25“As will appear later in more detail, the quantity of capital as a value magnitude, no less than the different investment periods, are not data, but are among the unknowns which have to be determined.” (Hayek 1941, 192)
- 26“The length of time expended in the past for the production of capital goods available today does not count at all. These capital goods are valued only with regard to their usefulness for future want-satisfaction. The ‘average period of production’ is an empty concept.” (Mises [1949] 1998, 486)
- 27“[Böhm-Bawerk’s] effective, although I think mistaken, critique of the earlier productivity theories of interest had the effect of causing later development to centre [sic] increasingly round the ‘psychological’ or ‘time-preference’ element in his theory rather than the productivity element.” (Hayek 1941, 42)
- 28“... Böhm-Bawerk in the elaboration of his theory did not entirely avoid the productivity approach which he himself had so brilliantly refuted in his critical history of the doctrines of capital and interest.” (Mises [1949] 1998, 486)
- 29The author wishes to thank an anonymous referee for the reference to and remarks about Faber’s work.
- 30In his recent presentation of The Pure Theory of Capital, Steele (2014) does not expound this model at all.
- 31“Of the two branches of the Böhm-Bawerkian school, that which stressed the productivity element almost to the exclusion of time preference, the branch whose chief representative is K. Wicksell, was essentially right, as against the branch represented by Professors F. A. Fetter and I. Fisher, who stressed time preference as the exclusive factor and an at least equally important factor respectively.” (Hayek 1941, 420)
- 32Writes Salerno (2001, 45): “However, in Austrian capital theory, each dose of net investment, ceteris paribus—and after a transition period during which the appropriate resource reallocations have been completed—brings about a stationary economy in which the new higher level of gross investment and the elongated structure of production is just sufficient to support a definite increase in the flow of consumer goods. As long as gross investment is maintained at its new higher level, the output of consumer goods per period will remain constant.” See also the recent qualified defense of Garrison’s theory of secular growth by Murphy (2017).
- 33“[P]erhaps the primary virtue of Time and Money is its exposition of capital-based macroeconomics in terminology and graphs that non-Austrian economists can understand.” (Murphy 2017, 353)


