ABSTRACT: Whenever risk managers are confronted with deep uncertainty and organized complexity, probabilistic inference methods which claim crisp inputs and precise results cannot be used effectively. This is a thesis of this paper which we derive from a systemic viewpoint and discuss in the context of praxeology. More specifically, our contribution to the literature of Austrian Economics is twofold. First, after revisiting the Knightian nomenclature of risk vs. uncertainty, which according to Hoppe (2007) is similar to Ludwig von Mises’s work on the subject matter, we present our own conception of risk which differs from their notion. Second, we follow Hoppe (2007) in assessing the arguments provided by Knight and Mises against the possibility of applying probability theory in the area of human action, but reach a different, more nuanced conclusion. In particular, we outline a case which parts ways with the praxeological approach.
KEYWORDS: Austrian economics, risk, uncertainty, complexity, probability
JEL CLASSIFICATION: B4, C1
Dr. Christian Hugo Hoffmann (choffmann@ethz.ch) is a postdoc at the Chair of Entrepreneurial Risks at the Swiss Federal Institute of Technology in Zurich (ETH), Switzerland.
Quarterly Journal of Austrian Economics 21, no. 3 (Fall 2018) full issue, click here.
It is high time, however, that we take our ignorance more seriously.
– (Friedrich A. Hayek, 1967)
1. INTRODUCTION
This paper characterizes and discusses different concepts of risk and seeks to define a proper meaning of the term in the realm of economics and finance. The purpose is not only to simply deepen our conceptual knowledge, but to, and this is particularly relevant to Austrianism, identify and examine the potential of going beyond the mere and rigid dichotomy of risk vs. uncertainty which Knight and Ludwig von Mises rely on. This is achieved by exploring if and how far systematization can be deemed possible in the non-probabilistic realm of uncertainty. Even though at the end we will also differentiate between Knightian risk and uncertainty (so to speak), it is important to note that we only endorse a single concept of risk which is different from Knightian risk and which will be baptized Risk I (section 5). We introduce Risk I in a deductive manner by postulating four requirements that a risk notion should meet (section 4). Prior to that, we review the literature (section 2) and turn the spotlight to Knight’s and Mises’ angle on risk (section 3). We close this paper in section 6 and 7 where we detail lessons from the taxonomy of risk we are proposing for Austrianism.
The absence of an accepted and appropriate definition of risk in the literature is not simply an abstract academic ivory tower issue. For example, risks in and to economic and financial systems are regarded as triggers of global financial crises (Schwarcz, 2008, pp. 193–249; Kelly, 1995, pp. 221ff.). Having lucid definitions is a fundamental requirement for management and modeling (Fouque and Langsam, 2013, p. xxviii). Without a well-thought notion of (financial) risk and approaches for measuring and managing the amount and nature of the risks, it would be difficult to effectively target indispensable (e.g., mitigating) action without running the real risk of doing more harm than good.
2. THE NOTION OF RISK IN THE LITERATURE
In non-technical contexts and contexts of common parlance, the word “risk” refers, often rather vaguely, to situations in which it is possible but not certain that some undesirable event will occur (Hansson, 2011; Heinemann, 2014).1 More precisely, the philosopher Sven O. Hansson distinguishes five particularly important and more specialized uses and meanings of the term, which are widely used across academic disciplines and/or in everyday language (Hansson, 2011).
(1) risk = an unwanted event which may or may not occur.
An example of this usage is: “The risk of a financial collapse is vast.”
(2) risk = the cause of an unwanted event which may or may not occur.
An example of this usage is: “Subprime lending is a major risk for the emergence of a housing bubble.” Both (1) and (2) are qualitative senses of risk. The word also has quantitative meanings, of which the following is the oldest one:
(3) risk = the probability of an unwanted event which may or may not occur.
This usage is exemplified by the following statement: “The risk that a financial collapse will occur within the next five years is about 70%.”
(4) risk = the statistical expectation value of an unwanted event which may or may not occur.
The expectation value of a possible negative event is the product of its probability and some measure of its severity. It is common to use the total amount of monetary costs as a measure of the severity of a financial crash. With this measure of severity, the “risk” (in sense 4) laden with a potential financial collapse is equal to the statistically expected number of monetary costs; i.e., for example, 70% (building on the example from (3)) times USD 10T results in USD 7T of expected overall costs of a global financial crisis. Other measures of severity give rise to other measures of risk.2
(5) risk = the fact that a decision is made under conditions of known probabilities (“decision under risk” as opposed to “decision under uncertainty”).3 See footnote 28 for an example.
All concepts of risk have in common what philosophers call contingency, the distinction between possible and actual events or possible and chosen action (Renn, 2008, p. 1). In addition to these five common meanings of “risk”, according to Hansson (2011), there are several other more technical meanings, which are well-established in specialized fields of inquiry. With regard to economic and particularly relevant analyses for the purposes of this study, nota bene that the current debate on risk resembles a Babylonian confusion of tongues. The present situation is characterized by many weakly justified and inconsistent concepts about risk (Aven, 2012, p. 33). Some of the many different definitions that are circulating are triaged and a subsumption system for them is given in Table 1. The purpose of this overview is to lay out the variety of material risk notions, rather than to claim that the categories proposed are exhaustive or mutually exclusive.
Table 1: Classification system for risk definitions and characterization of different risk definition categories.4
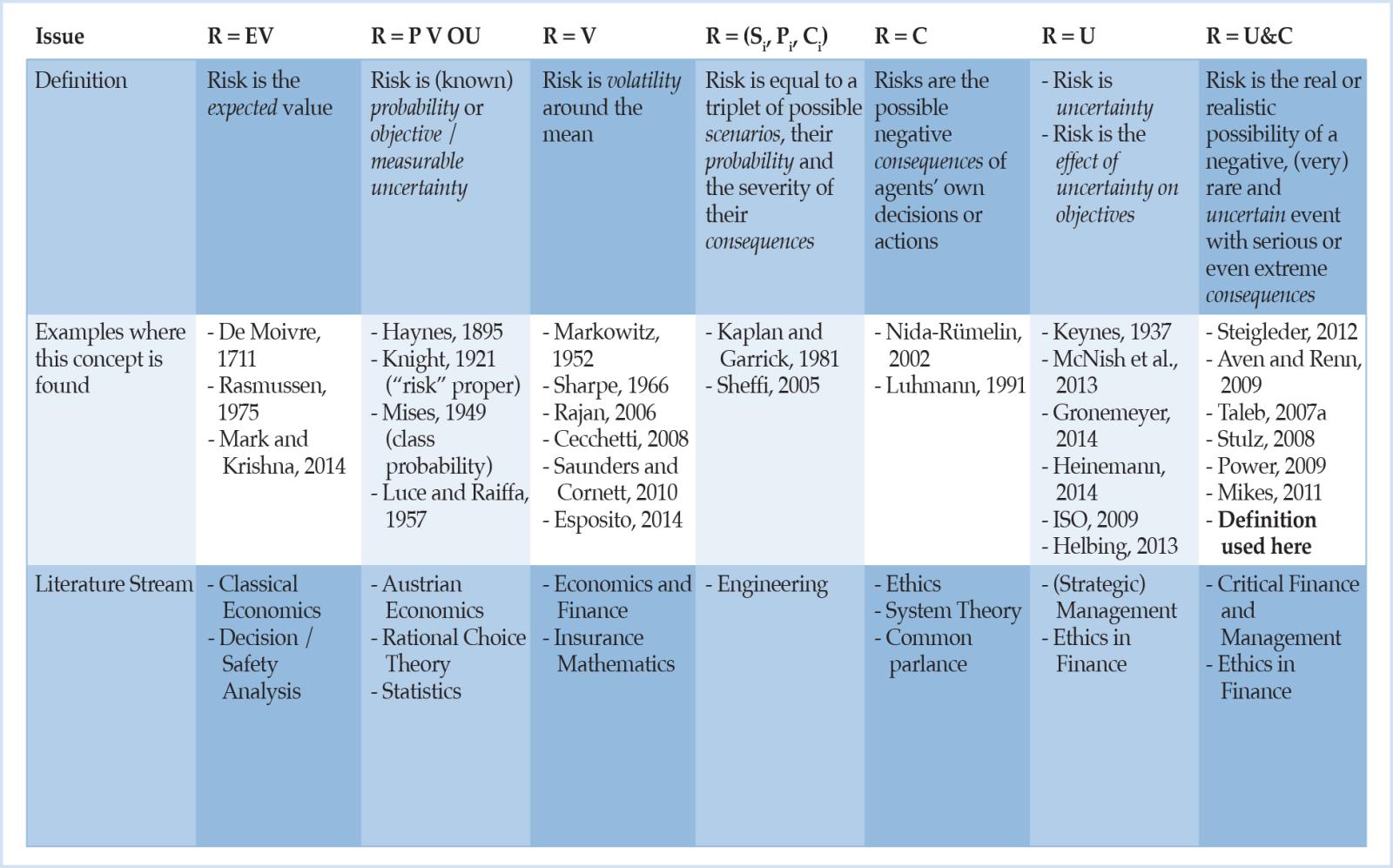
In light of this ambiguity, the next section pays special attention to how the term “risk” has been coined by the Austrian school of economics, by Ludwig von Mises and Frank Knight in particular.
3. THE NOTION OF RISK IN AUSTRIANISM
Hoppe (2007) deserves credit for investigating a systematic, yet rarely noted similarity in the works of Knight (1921) and Mises (1949), namely in terms of their stance on risk, uncertainty and (the scope of) probability (theory).5 However, the similarity concerns more than he spells out. Hoppe’s conclusion is not sufficiently satisfying because it remains incomplete when he simply notes that both Knight and Mises share a similar critical view on the limitations of mathematical probability theory, which would not prove to be useful in our daily endeavors of predicting human action (Hoppe, 2007, p. 19). Leaving that for the moment, Hoppe fails to discuss an intriguing shortcoming from which both oeuvres suffer. Knight (1921, ch. 7 and 8) and Mises (1949, ch. 6) treat the notions of uncertainty and probability, which are a primary concern of praxeology, but both treatments lack some conceptual clarity. To be precise, we do not disagree with Hoppe’s or Knight’s / Mises’s critical attitude towards the applicability of numerical or Kolmogorovian probability theory. Rather, the aforementioned lack of conceptual clarity on risk notions refers to a naïve identification of risk with (a frequency interpretation of) probability both Knight and Mises succumb to and which is not critically appraised by Hoppe.
Knight (1921, pp. 223f.) spots empirical-statistical probabilities and defines them as “insurable” contingencies or “risk.” Mises concurs with him (Hoppe, 2007, p. 11). Yet, why is this approach naïve? In section 4, we will call it problematic because it does not meet the first, second and third of four requirements which we will establish regarding an appropriate concept of risk. On top of that, the frequency interpretation of probability itself is laden with inconsistencies (cf. Hájek, 2011 for a synopsis). Therefore, by anticipating the reasoning underlying criteria 1 to 3 in section 4 and by pointing to the objections to frequentism in the literature, we are justified in stating the first of two research gaps.
Research Gap I: Poor conceptualization of the term “risk” as well as knowledge deficits concerning the conceptual relationships between “risk,” “uncertainty,” and “probability” in a finance and economics context.
Mises (1949, pp. 107ff.) actually does not even single out “risk” as a terminus technicus in this connection of elaborating on the interpretations of probability. Instead, he first comments rather vaguely:6
A statement is probable if our knowledge concerning its content is deficient. We do not know everything which would be required for a definite decision between true and not true. But, on the other hand, we do know something about it; we are in a position to say more than simply non liquet or ignoramus. (Mises, 1949, p. 207).
Within this wide, general, and under-determined class of probabilistic statements, Mises then distinguishes two categorically distinct subclasses. The first one—probability narrowly understood and permitting the application of the probability calculus—bears the signature of his brother Richard, who first and foremost coined the objective concept of probability (Mises, 1939), and is called “class probability”:7
Class probability means: We know or assume to know, with regard to the problem concerned, everything about the behavior of a whole class of events or phenomena; but about the actual singular events or phenomena we know nothing but that they are elements of this class. (Mises, 1949, p. 207).
On the other hand, Knight (1921, pp. 223f., 226, 231f.) calls the other sort of contingency (i.e., probabilities which are not a priori or empirical-statistical) “true uncertainty” and describes it as an estimate or intuitive judgment. For example, business decisions “deal with situations which are far too unique, generally speaking, for any sort of statistical tabulation to have any value for guidance. The conception of an objectively measurable probability or chance is simply inapplicable.” (Knight, 1921, p. 231). Almost three decades later, Mises (1949, p. 110) adds that true uncertainty or case probability, which is how he refers to it, means:
We know, with regard to a particular event, some of the factors which determine its outcome; but there are other determining factors about which we know nothing. Case probability has nothing in common with class probability but the incompleteness of our knowledge. In every other regard the two are entirely different. (Mises, 1949, p. 110).
In particular, while the probability calculus is only applicable to ‘genuine’ classes or collectives (hence the name class probability), case probability is about individual, unique, and non-repeatable cases/events “which as such—i.e., with regard to the problem in question—are not members of any class” (Mises, 1949, p. 111). Thus, they lie outside the scope of classical probability theory. Yet, what kinds of events must be considered as instances of case probability according to Mises? He provides the reader with the following initial answer:
The field for the application of the former [class or frequency probability] is the field of the natural sciences, entirely ruled by causality; the field for the application of the latter [case probability] is the field of the sciences of human action, entirely ruled by teleology. (Mises, 1949, p. 107).
It follows that “human action is the source of ‘true,’ nonquantifiable (Knightian) uncertainty” (Hoppe, 2007, p. 11). We share Hoppe’s observation that, unfortunately, Mises (1949) is less than outspoken in elucidating why human actions (choices) are intractable by probability theory (in the frequency interpretation) (ibid.). Moreover, we claim however that Hoppe’s intended main contribution in his paper, namely to render the reason why choices are intractable by the frequency interpretation of probability explicit based on the Misesian framework, is insufficient and provide evidence in section 6. To put it in a nutshell already, we will not accept Hoppe’s rationale because we reject the Misesian framework for this particular purpose. Instead, we will bring forward Proposition II and, thereby, ground the matter of the scope and limitations of probability theory on questions on complexity in lieu of human action. For now, we acknowledge
Research Gap II: Lack of understanding of whyhuman action and choices lie outside the scope of classical (Kolmogorovian) probability theory.
We address those two research gaps in the following. Section 6 seeks to close research gap II although the proposition that human action per se cannot be captured by probability statistics turns out to be untenable. Section 5 targets research gap I and the very next chapter constitutes a necessary stepping stone in this direction. Put differently, some notes on the epistemology of risk are in order first to escape possible snares before we deduce our own definition of risk.
4. THE EPISTEMOLOGY OF RISK
When there is a risk, there must be something that is unknown or has an unknown outcome. Therefore, knowledge about risk is knowledge about lack of knowledge (Hansson, 2011). This combination of knowledge and lack thereof contributes to making issues of risk difficult to grasp from an epistemological point of view.
Second, it is sensible to acknowledge that risk not simply refers to something unknown, but to draw a conceptual framework distinguishing between the known, the unknown, and the unknowable (“KuU” as it is labeled by Diebold et al., 2010). Accordingly, Kuritzkes and Schürmann (2010, p. 104) call a risk known (K) if it can be identified and quantified ex ante; unknown (u) if it belongs to a collective of risks that can be identified but not meaningfully quantified at present;8 and unknowable (U) if the existence of the risk or set of risks is not anticipatable, let alone quantifiable, ex ante. Nota bene: there is no sharp definitional line to be drawn between these classes, maybe leaving the KuU classes lying along a continuum of knowledge.
Third, things are even more confusing because even “known” risks (in the sense of Kuritzkes and Schürmann, 2010) contain uncertainty: “[…] as recent evidence coming from the financial markets painfully shows, the view according to which a ‘known probability distribution’ contains no uncertainty is not quite right” (Fedel et al., 2011, p. 1147).1 The authors strengthen their assertion as follows (Fedel et al., 2011, p. 1147): Suppose a die is being rolled. One thing is to be uncertain about the face that will eventually show up (a “known” risk). One quite different thing is to be uncertain about whether the die is fair or unbiased (is the ostensibly known risk really known?) (Fedel et al., 2011, p. 1147). In other words, we can rather naturally differentiate between first order and second order uncertainty, respectively. In the former case, we are uncertain about some (presently unknown) state of affairs. In the latter, we are uncertain about our uncertainty, i.e., second order uncertainty refers to the assessment that an agent makes about her own uncertainty (Fedel et al., 2011, pp. 1147f.).10
Finally, fourth, Hansson (2011) observes that a major problem in the epistemology of risk, a problem which is paid special attention to in this study, is how to deal with the severe limitations that characterize our knowledge of the behavior of unique complex systems that are essential for estimates of risk (e.g., modern financial systems). Such systems contain components and so many, potentially shifting, interactions between them that it is in practice unpredictable (Hansson, 2011).
These four points already presage that the relationship between the concepts “risk,” “knowledge,” and “uncertainty” seems to be wide-ranging, multi-layered and elusive. Hereafter, we try to cope with these issues and, further, to establish four explicit conditions for defining a proper, i.e., a more useful and a consistent,11 notion of risk.
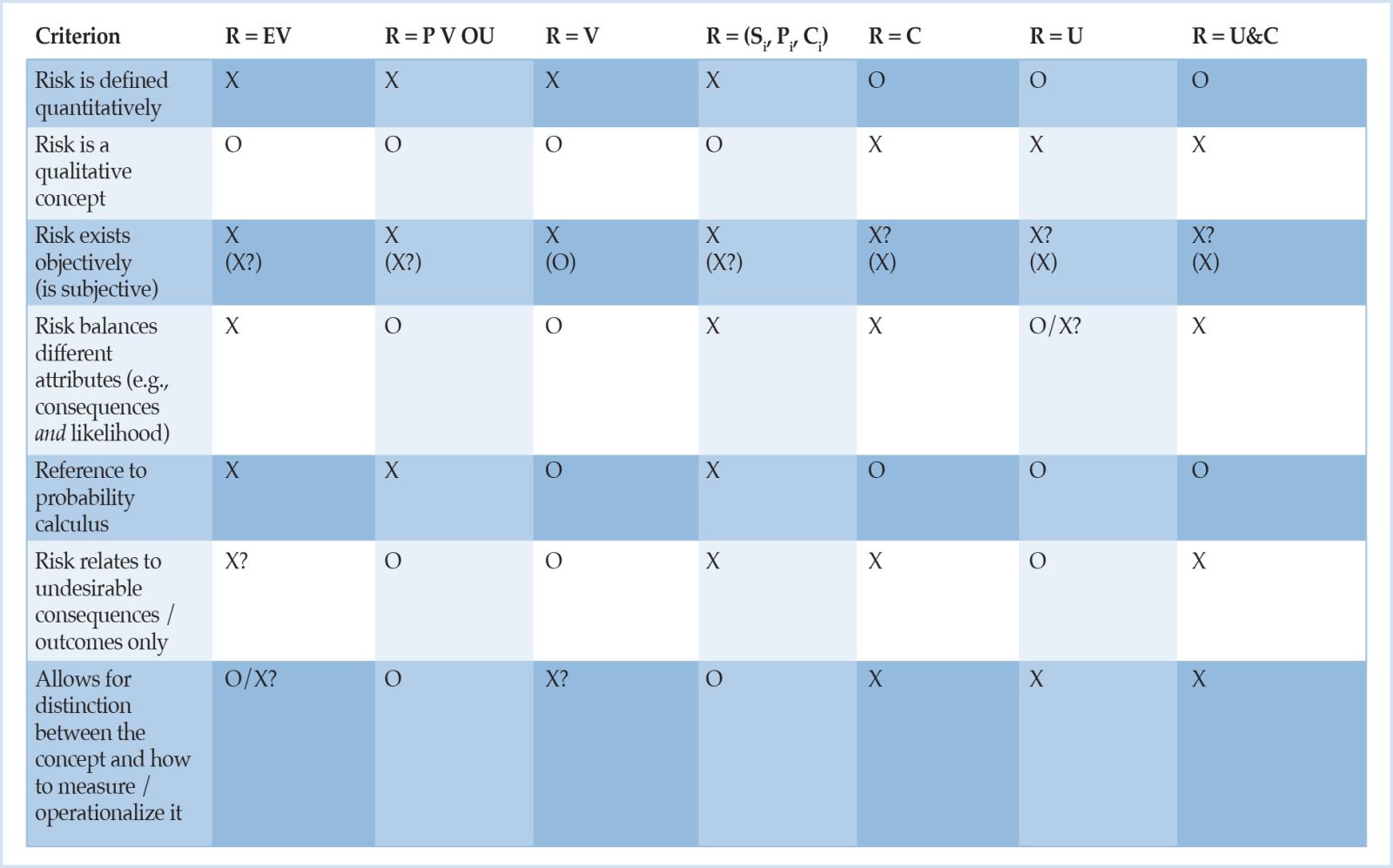
Condition 1: Risk should be defined in such a way that it can be distinguished between risk per se (what risk is) and how risk is measured, described or managed (Aven, 2012, p. 33; Bradley and Drechsler, 2014, p. 1226).
Rationale: This condition is important because there exist perspectives on risk in which this distinction is not made (see Table 1 and cf., e.g., Beck, 1992, p. 21; Hansson, 2007, p. 27). Like MacKenzie (2006, pp. 143–179), George Soros (2008, p. 3) notes how “our understanding of the world in which we live is inherently imperfect because we are part of the world we seek to understand” and he focuses on “how our knowledge of the world is interdependent with our measurements of it” (Blyth, 2010, p. 460).12 In principle, every (measurement or description or management) tool in use (which could be based on stochastic models) should be treated as such. Every such tool has its limitations and these must be given due attention. By a distinction between risk as a concept, and its descriptions or assessments “we will more easily look for what is missing between the overall concept and the tool” (Aven, 2012, p. 42). By the same token, if a proper framework clarifying the disparity between the overall risk concept, and how it is being measured or operationalized etc. is not established, it is difficult to know what to look for and how to make improvements in these tools (Aven, 2012, p. 42). In addition to that, it is a central principle of systems science, which in turn is in consonance with the Austrian line of thought,13 to examine issues from multiple perspectives—“to expand the boundaries of our mental models” (Sterman, 2000, p. 32)—and, as a consequence, the risk concept should not be illuminated by one theoretical perspective only (e.g., mere probabilistic underpinnings); it should not be founded on one single measurement tool. Because in the various scientific environments, application areas or specific contexts, there might not be one best way to measure/describe risk. This appears to be, therefore, a reasonable and uncontroversial premise which can be further strengthened by an analogy to the Austrian debate on the single concept “utility” that has been operationalized in different ways. One camp around Böhm-Bawerk would maintain a cardinal understanding of utility, namely that the utility of goods can be measured and expressed as a multiple of a unit. By contrast, Čuhel, Mises, and many more would defend an ordinal understanding of utility (Moscati, 2015). Thus, once we allow for the distinction between utility and its measurement, we enable both and potentially other parties to talk sense about utility from different angles, to elaborate on different facets of the broad notion, and so forth (be it a cardinal utility function or an ordinal understanding).
Application to Knightian/Misesian framework: When Knight (or Mises, for that matter) identifies risk with (a frequency interpretation of) probability, he does not pass this test because then it is not differentiated between the notion (i.e., risk and hence probability) and its operationalization (i.e., the probability measure).
The second condition purports the following:
Condition 2: Risk should be defined in such a way that it can be distinguished between what risk is and how risk is perceived (Aven, 2012, p. 34)14 as well as that the definition does not presuppose an interpretation of either objective or subjective risk (Hansson, 2011).
Rationale: There is a major debate among risk professionals about the nature of risks: are risks social or subjective constructions (human ideas about reality, a feature of the agent’s informational state) or real-world, objective phenomena (representations of reality, a feature of the world itself;). Willett (1901) and Hansson (2011), for example, speak up for a strong objective component of risk: “If a person does not know whether or not the grass snake is poisonous, then she is in a state of uncertainty with respect to its ability to poison her. However, since this species has no poison there is no risk to be poisoned by it” (Hansson, 2011). On the other hand, it is obvious to others that risks constitute mental models (Renn, 2008, p. 2). They are not veritable phenomena, but originate in the human mind (Renn, 2008, p. 2). As Ewald (1991, p. 199) notes: “Nothing is a risk in itself; there is no risk in reality. […] [A]nything can be a risk; it all depends on how one analyses the danger, considers the event.” The definitional framework should, hence, try to “avoid the naïve realism of risk as a purely objective category, as well as the relativistic perspective of making all risk judgments subjective reflections of power15 and interests” (Renn, 2008, p. 3).
Application to Knightian/Misesian framework: Needless to restate the well-known objections to objective probabilities (e.g., cf. Hájek, 2011 for an overview), but interestingly, since Knight and Mises embrace a frequentism-based notion of probability, they also seem to endorse a purely objective interpretation of “risk.” Thus, their framework does not pass this second test either. At least, some more clarification would be required because, on the other hand, subjectivism is considered a central pillar for economists of the Austrian School (e.g., Spitznagel, 2013, pp. 21, 76). Or maybe it simply follows then that an agnostic position should be taken as Condition 2 suggests it.
There are at least two more requirements for a good risk definition.
Condition 3: Risk should be defined in such a way that it is helpful to the decision-maker in lieu of misguiding her in many cases (Aven, 2012, p. 42), and, thereby, the risk definition should capture the main pre-theoretic intuitions about risk (Rothschild and Stiglitz, 1970, p. 227).
Rationale: At first glance, this condition might sound trivial, but it must not be forgotten that risk cannot be confined to the ivory tower of scholarly deliberations. Even though it might be a theoretical and abstract concept, risk has forged a direct link with real-life management of challenges and actual decision-making. It has a direct impact upon our life and the orientation along decision-making and human action is key for Austrianism (Mises, 1949) as well. Speaking for the banking context, banks, taxpayers, governments lost a lot of money (and much more; e.g., credibility) because risk managers (in a broad sense) ignored or misjudged risks, miscalculated the uncertainties or had too much confidence in their ability to master dangerous situations (FCIC, 2011). Ultimately, only time and feedback from the economic practice can tell whether or not this premise is fulfilled.
Application to Knightian/Misesian framework: Some proposals such as R = P V OU, i.e., the framework of Mises, 1949 and Knight, 1921 (see Table 1), do not fulfill this criterion because, to put it in the words of Aven (2012, p. 41), “referring to risk only when we have objective distributions would mean we exclude the risk concept from most situations of interest.” Thus, this risk concept would not prove helpful in many or most cases of decision-making.
In conjunction to this third premise, opening the debate to a wider (namely, to a non-academic) audience, one can also see the following ethical demand.
Condition 4: Risk should be defined in such a way that it does not divert attention away from systemic effects that have an impact on not only the actor, but also on other actors (Rehmann-Sutter, 1998, p. 120).
Rationale: The school of Austrian economics also emphasizes the importance of systemic effects that are usually associated with (very) low-frequency events in a high-dimensional space—cf. for example, Spitznagel, 2012: “The Austrians and the Swan: Birds of a Different Feather.” Yet, Rehmann-Sutter (1998, p. 122) goes one step further and bemoans the fact that in some economic concepts of risk, “there is only one personal position: the decision-maker,” whereas most risks are not individual but rather social (Sen, 1986, pp. 158f.), i.e., there might be negative consequences for others from “taking risks.” He adds, however, that we have difficulty in adequately including those other persons (e.g., taxpayers in our context) affected by the consequences of the (risk management) decision (of a bank) in the decision-making process, where the concept of risk is worked out in reality (Rehmann-Sutter, 1998, p. 122). “These other participants are abstract; attention is diverted away from them. These participants are conceptually hidden” (Rehmann-Sutter, 1998, p. 122).
Application: We cannot regard this critique as fundamental in terms of the economic risk concepts taken into consideration in Table 1—e.g., the definition R = EV does not entail a narrow reading of the consequences. Therefore, we consider 4 as a weak condition which can in principle be met by every risk definition. In other words, condition 4 is more about the interpretation of the definition than about the risk definition itself. Nevertheless, an important lesson can be learned from that admonition, among the most prominent of which was drawn by Kristin Shrader-Frechette.
Shrader-Frechette (1991) points to the unease we feel when we are using a concept which was elaborated for optimization of entrepreneurial behavior in an unpredictable market to describe interventions into the (financial) system with potential or actual adverse effects to other persons and institutions. What is prima facie rational might secunda facie not be rational if a feedback view of the world is adopted (Sterman, 2000). Since only those risks enter standard probabilistic risk measurement procedures that (directly!) affect the respective organizations, risk managers or traders etc. often do not see a direct connection between their actions and other actors (Garsten and Hasselström, 2003, p. 259) or with significant changes in the financial system or even the global economy, which, in the end, bounce back on the individual institutions themselves.
For now, a first bottom line is that, unfortunately, many extant definitions of risk do not even meet the first two basic requirements (see Table 1, rows 3 and 7). In terms of Table 1, only risk in the sense of uncertainty (R = U) and risk as the real or realistic possibility of a negative, (very) rare and uncertain event with serious or even extreme consequences (R = U&C) remain in the game. Since seeing risk as uncertainty can be considered a special case of U&C, the latter seems to be the most promising candidate whereas the other risk concepts presented do not only turn out to not have some desirable properties, but also suffer from other shortcomings. For example, the especially in a banking context relevant identification of risk with volatility or the variance of returns (R = V) is clearly unsatisfactory: “We can construct distributions that have identical variance but with which we would associate very different degrees of ‘riskiness’ – and risk, as the saying goes, is one word but is not one number” (Rebonato, 2007, p. 237; cf. also Rootzén and Klüppelberg, 1999); “[i]n any case, anyone looking for a single number to represent risk is inviting disaster” (Taleb et al., 2009, p. 80; cf. also Power, 2007, p. 121).
Before we shed some more light on U&C, it makes sense to first look closer at another example, namely the field of the risk definition R = P V OU where Mises (1949) and Knight (1921) made one of the first large-scale distinctions between risk and uncertainty, for what became known as ‘Knightian risk’ (= measurable uncertainty) and ‘Knightian uncertainty.’ Albeit there might be good reasons for regarding Knight’s original argument for distinguishing between risk and uncertainty as going astray (see condition 3),16 it is nevertheless important to bear it in mind due to several reasons.
First, it is very puzzling to see how different economists, risk experts and others have reacted to Knight’s oeuvre, how they interpreted it and what conclusions have been drawn. A good example is that while both the critical finance community (e.g., Stout, 2012; Bhidé, 2010; Aven and Renn, 2009; Power, 2007; or Taleb and Pilpel, 2004), on the one hand, and the economic (imperialistic) mainstream (Friedman, 1976; Ellsberg, 1961; Savage, 1954) on the other, consider Knight’s distinction between risk and uncertainty as invalid because his risk perspective is too narrow, the interests of these two groups are diametrically opposed to each other: Whereas the former repels probability based definitions of risk (“risk as a concept should not be founded on one specific measurement tool [such as probability—C.H.],” Aven, 2012, p. 42) in favor of uncertainty, the latter maintains that Knightian risk, i.e. risk measured by probability, would prevail instead of “uncertainty” (“for a ‘rational’ man all uncertainties can be reduced to risks [because it is believed that we may treat people as if they assigned numerical probabilities to every conceivable event—C.H.],” Ellsberg, 1961, p. 645).17
Second, Knight’s seminal work might, therefore, be seen as very influential or even path-breaking for the more recent history of economic thought (Heinemann, 2014, pp. 61f.; Aven, 2012, p. 41; Esposito, 2011, p. 32) and as laying the grounds for a common meaning of “risk” (Hansson, 2011), especially relevant in economics and decision theory (Luce and Raiffa, 1957). Indeed, the tie between risk and probability is seen as so strong that only few seem to question it: “Risk can only be found in situations that have to be described by probabilities” (Granger, 2010, p. 32). Moreover, Knight (1921) introduced a simple but fundamental classification of the information challenges faced in banks’ risk management, between Knightian risks which can be successfully addressed with statistical tools (Value at Risk, Expected Shortfall, etc.), and Knightian uncertainties which cannot (Brose et al., 2014, p. 369). Good risk management, thus, calls for toolkits that handle both Knightian risk and uncertainty (Brose et al., 2014, p. 369).
Hence, third, it is important to have a risk concept based on probability models to be able to participate in, and contribute to, the discourse of risk if a great number of participants and economists or people interested in risk management in banking, in particular, should be reached. Since such a definition of risk (which will be baptized Risk II) would not do justice to the requirements set above (e.g., the first condition), however, it will not be the one which is pursued and embraced in this study after all.
Hence, it would be premature to simply and uncritically take on Taleb and Pilpel’s (2004) or Aven’s (2012) position of pleading in favor of leaving the Knightian nomenclature once and for all. Instead, our strategy is twofold. We first conclude that the kind of definitions by Heinemann (2014), Steigleder (2012), Aven and Renn (2009), etc. are the most appropriate before we approve a narrow notion of risk that is compatible with how risk discussions are commonly held.
5. UNDERSTANDING RISK
As an answer to research gap I, risk, in this paper, is paraphrased broadly as18
… the real or realistic possibility of a positive or negative event the occurrence of which is not certain, or expectable19 but only more or less likely. However, the probability that the positive or negative event will occur does not have to be known or be subject to exact numerical specification.
Thus, the term “risk” is not used as an antonym to “uncertainty”, as is customary in decision theory, but rather as a generic concept that covers both “risk in a narrower sense” (what Knight, 1921, calls measurable uncertainty) and “uncertainty”. This is because we frequently lack a sufficient basis to determine the probabilities with any precision (Greenbaum, 2015, p. 165) as it will be clarified below.
This broad notion of risk is designated by Risk I. Structurally, risk in this sense captures:
- What can happen?
- Answering this question requires the identification or description of consequences or outcomes of an activity.
- Is it more or less likely to happen (in contrast to how likely is that to happen)?
- Attention is directed to rather rare or systemic events in this piece for reasons that become transparent below.
- If it does happen, what is the impact?
- Answering this question requires the evaluation of consequences which are rather serious or even extreme. Otherwise, risks would turn out to be immaterial.
We thereby follow the call of Das et al. (2013, p. 715) that risk management research will have to dig deeper “in going from more frequency oriented ‘if’ questions to a more severity oriented ‘what if’ approach, and this at several levels”. In this particular treatise, the focus lies on (very) low-frequency events in a high-dimensional space or, in particular, on low-frequency, high-severity (monetary) losses for several reasons. For example, pushing natural phenomena to an extreme unveils truths that are ensconced under normal circumstances. As stressed in Johansen and Sornette (2001) and following the 16th century philosopher Francis Bacon, the scientific appeal of extreme and systemic events is that it is in such moments that a complex system offers glimpses into the true nature of the underlying fundamental forces that drive it (Johnson et al., 2012, p. 3).
Accordingly, the need to address unexpected, abnormal or extreme outcomes, rather than the expected, normal or average outcomes is a very important challenge in risk management (McNeil et al., 2005, p. 20; Malevergne and Sornette, 2006, p. 79; Greenbaum, 2015, p. 164); because improving the comprehension (of the distribution) of extreme values, which cannot be dismissed as outliers because, cumulatively, their impact in the long term is dramatic, is of paramount importance (Mandelbrot and Taleb, 2010).20
Benoît Mandelbrot uses a nice metaphor for illustration’s sake (cf. also Churchman, 1968, p. 17): “For centuries, shipbuilders have put care into the design of their hulls and sails. They know that, in most cases, the sea is moderate. But they also know that typhoons arise and hurricanes happen. They design not just for the 95 percent of sailing days when the weather is clement, but also for the other 5 percent, when storms blow and their skill is tested.” (Mandelbrot and Hudson, 2008, p. 24). And he adds: The risk managers and investors of the world are, at the moment, like a mariner who “builds his vessel for speed, capacity, and comfort—giving little thought to stability and strength. To launch such a ship across the ocean in typhoon season is to do serious harm.” (Mandelbrot and Hudson, 2008, p. 276).
Clearly, this does not mean that (very) low-probability risk events matter simply because they have a very low probability. For example, there is some probability that a pink elephant will fall from the sky. But such a risk does not affect managerial decisions in economic and financial systems (such as banks). The known or unknown risks that matter for our purposes are, of course, those that, had senior or top management been aware of them, would have resulted in different actions (Stulz, 2008, p. 64)—e.g., the bursting of a pricing bubble or an escalating political conflict etc.
Second, a narrow concept of risk is invoked (Risk II); it is basically circumscribed by two key variables, the severity of the consequence and its probability of occurrence,21 and it presupposes that possible/significant consequences and the corresponding values of severity and probabilities are known.22 2 Risk II encompasses Hansson’s (2011) risk definitions 3 to 523 and it can be regarded as a special and rare case of the broad risk definition (Risk I). Figure 1 depicts the conceptual relationships between Risk I, Risk II, and uncertainty, and can be viewed as our proposal to close research gap I.
Figure 1: Two relevant risk concepts: Risk I encompasses Risk II and uncertainty.24
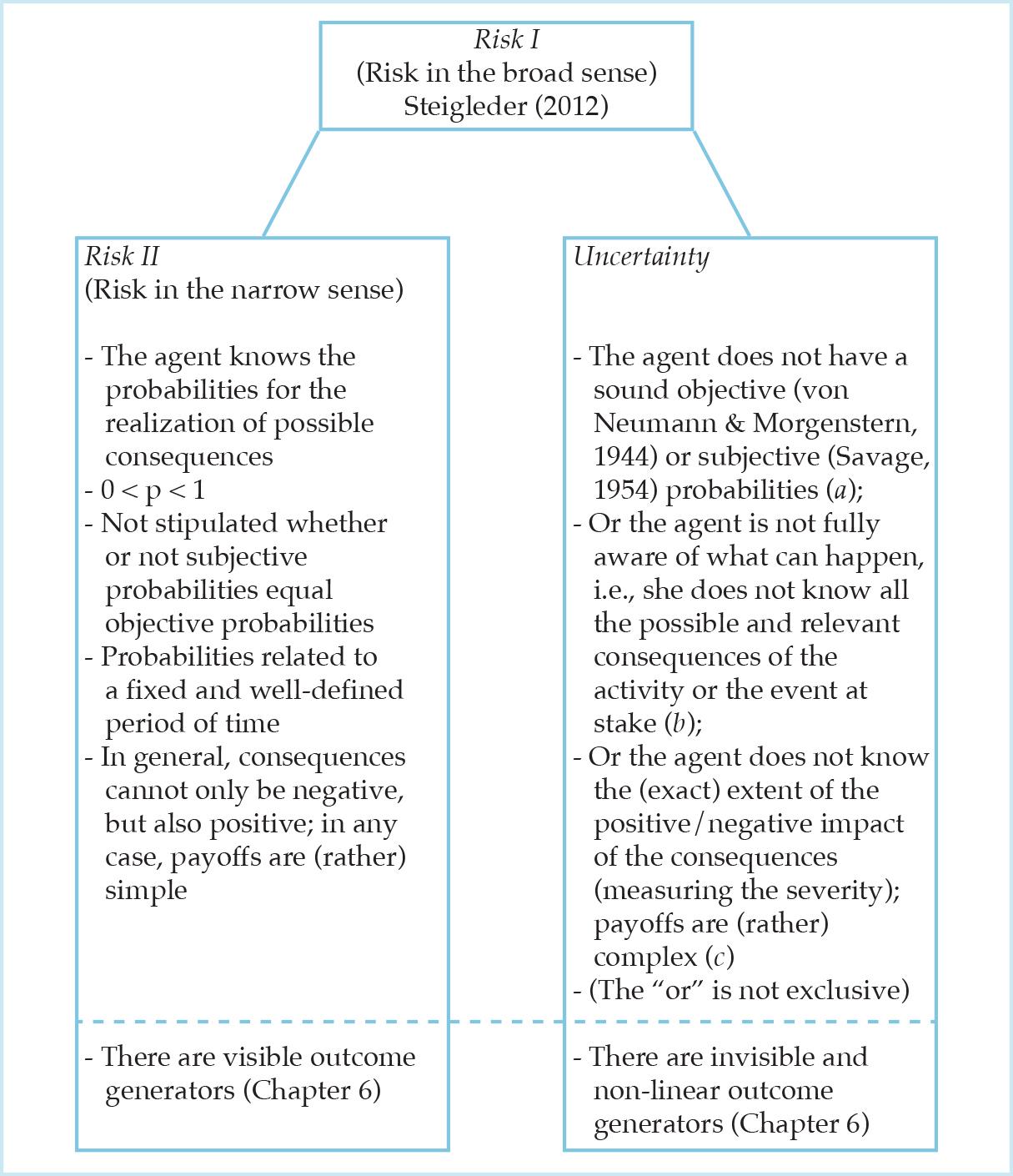
Risk II is rather hypothetical or an exception and this case is basically constructed only to participate in regular risk discussions (see above, p. 15).25 Apart from the different orders of uncertainty (Fedel et al., 2011, p. 1147; Ellsberg, 1961), different types of uncertainty need to be taken into account. In Figure 1, we distinguish three qualitatively different types of uncertainty: (a) what decision theorists or philosophers might call state uncertainty, (b) what they might call option uncertainty and/or state space uncertainty, and (c) what corresponds to ethical uncertainty, a form of normative uncertainty (cf. Bradley and Drechsler, 2014). On top of that, many different kinds of risk (business risk, social risk, economic risk, etc., Kaplan and Garrick, 1981, p. 11) or categories of risk (market, credit, operational risk, etc.) are discussed in the literature and many more classification systems are introduced. We argue, however, that, even though some of the taxonomies offered for bank risks or for knowledge (or the lack thereof) are persuasive, e.g., the conceptual framework “KuU” by Diebold et al. (2010), at least the silo-treatment of risks should be overcome. Instead of devoting much attention to different forms of risk, the focus lies here on R = U&C in general. The broad concept of risk is chosen as a form of description since it is not a priori clear for concrete risks at issue whether or not the probabilities and potential consequences as well as their severity are known. Knight’s (Mises’s) important distinction between risk and uncertainty is esteemed by separating Risk II from uncertainty. This differentiation is, in some cases, indispensable for the discourse of risk (management) in banking because different implications arise: The risk perspective chosen strongly influences the way risk is analyzed and, hence, it may have serious effects on risk management and decision-making (Aven, 2012, p. 42). However, much of what we today call risk management is “uncertainty management” in Knightian terms, i.e., courageous efforts to manage ‘risk objects’ for which probability and outcome data are, at a point in time, unavailable or defective (Power, 2007, p. 26; Willke et al., 2013, p. 9).
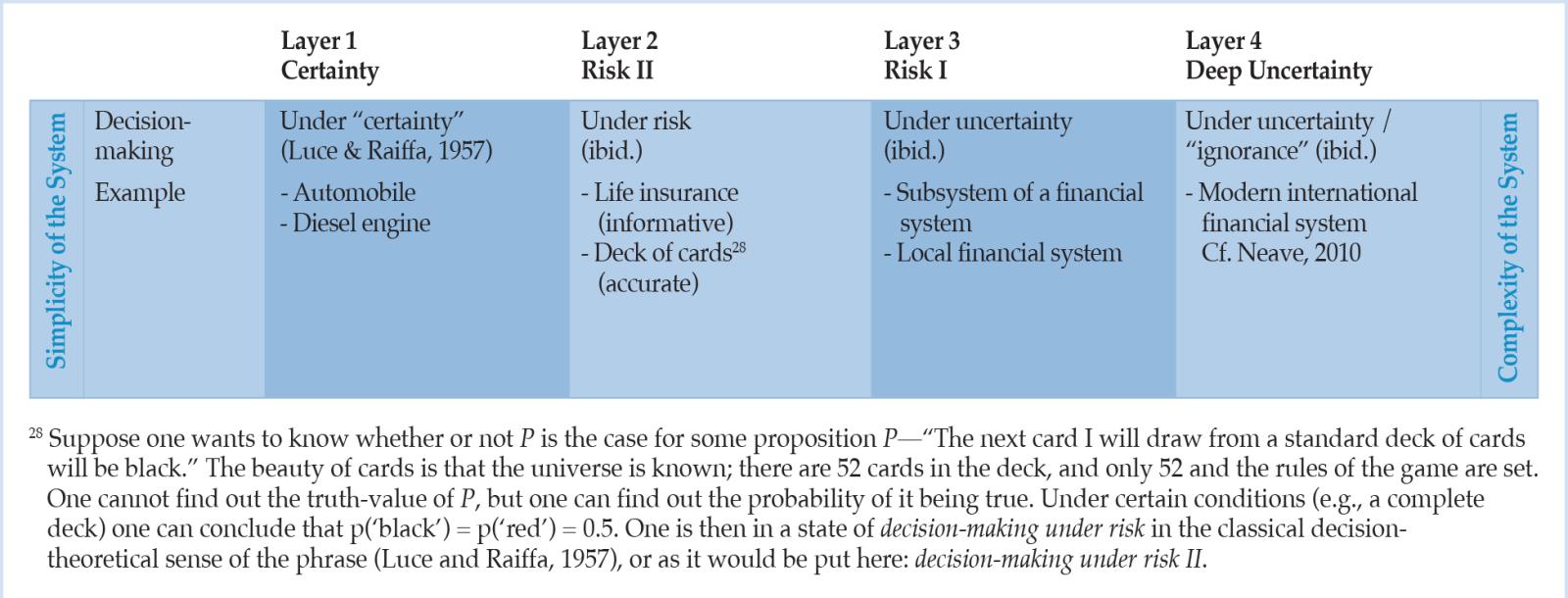
6. A TAXONOMY OF UNCERTAINTY: SCALES OF MEASUREMENT AND QUANTITATIVE VS. QUALITATIVE PROBABILITIES
It is a commonplace that we must not undertake impermissible transformations on the data we wish to analyze, nor must we make interval statements on ordinal data, in particular (Flood and Carson, 1993, pp. 41f.).26 We agree with Mises (1949, p. 113) that there is a form of uncertainty, which he calls case probability and we will call deep uncertainty, and which does not lend itself to classical probability-based methods: “Case probability is not open to any kind of numerical evaluation” (Mises, 1949, p. 113). On this basis, we hypothesize that when we as risk modelers are in a state of deep uncertainty about some future data or events, then we can perform, not a cardinal, but an ordinal ‘measurement’ of that risks only.27 In other words freely adapted from the logician and philosopher W.V.O. Quine, cardinalists’ overpopulated universe offends the aesthetic sense of us who have a taste for desert landscapes. Their aspiration after pedantic preciseness abets a breeding ground for disorderly mathematical operations on data and risks that necessitate modesty.
Proposition 1: Deep uncertainty or case probability does not admit of degrees, but is a merely comparative notion.
However, we do not agree with Mises (1949) about the scope of case probability vs. deep uncertainty. While he claims that “[c]ase probability is a particular feature of our dealing with problems of human action” (Mises, 1949, p. 111) and, thus, that human action and choices lie outside the scope of classical (Kolmogorovian) probability theory, Mises remains short on providing us with a sufficient reason for this assertion (see research gap II).
Our strategy by contrast is twofold: We suggest that the class of human choices and actions is both too broad and too narrow for capturing uncertainty statements that cannot be expressed in probabilistic terms. It is too broad because we can reason about human action and choices probabilistically (see “decision-making under risk,” Luce and Raiffa, 1957, or Table 1 [the column in the middle] below). Admittedly, it can be argued that all decisions are made “under uncertainty” if one abstracts from clear-cut and idealized textbook cases, but if a decision problem is treated as a decision “under risk” (e.g., the probability of rain is 70 percent [according to the weather forecast]; shall I take an umbrella to work?), this does not mean, as Hansson (2011) clarifies, that “the decision in question is made under conditions of completely known probabilities. Rather, it means that a choice has been made to simplify the description of this decision problem by treating it as a case of known probabilities. This is often a highly useful idealization in decision theory” yet it is, at the same time, important to distinguish between those probabilities that can be treated as known and those that are genuinely uncertain.
The class of human choices and actions is also too narrow because what some (not all) human actions and choices intractable by probability theory is organized complexity (Weaver, 1948), as we argue below, and organized complexity characterizes many different systems, not only human action.
Proposition 2: Deep uncertainty emerges from highly organized and dynamic complexity.
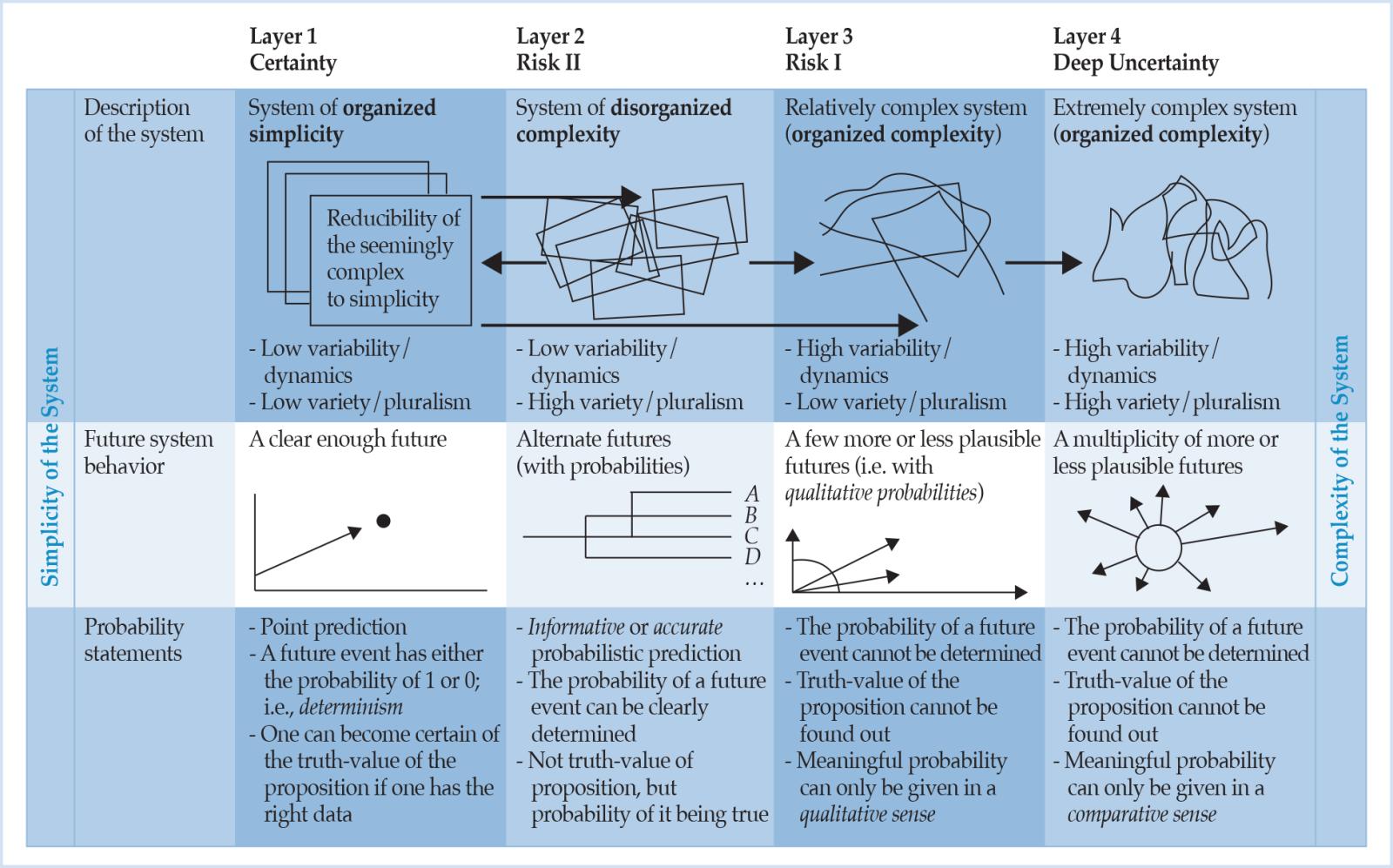
In a classic and massively referenced article, Weaver (1948) distinguishes three significant ranges of complexity, which considerably differ from each other in the mathematical treatment they require. He offers a classification that separates simple, few-variable problems (or a small number of significant factors) of ‘organized simplicity’ at the one end from the ‘disorganized complexity’ of numerous-variable problems at the other, where the variables exhibit a high level of random behavior. This leaves ‘organized complexity’ sitting between the two extremes. The importance of this middle region does, however, not depend primarily on the fact that the number of variables involved is moderate—large compared to two, but small compared to the number of atoms in a pinch of salt. The hallmark of problems of organized and dynamic complexity lies in the fact that these problems, as contrasted with the disorganized situations where statistical or probabilistic methods hold the key, show the essential feature of organization (Weaver, 1948, p. 539). This in turn involves dealing simultaneously with a sizable number of factors which are interrelated to form an organic whole. Interactions and the resulting interdependence lead to emergence, i.e., to the spontaneous appearance of features that cannot be traced to the character of the individual system parts (Anderson, 1972), and, therefore, cannot be fully captured in probability statistics nor sufficiently reduced to a simple formula. Something more is needed than mathematical analysis or the mathematics of averages (Weaver, 1948, p. 540; Huberman and Hogg, 1986, p. 376).
Weaver (1948, p. 539) lists examples of problems of organized complexity where in each case a substantial number of relevant variables is involved that are varying simultaneously, and in subtly interconnected ways. In particular, the economic, but not only the realm of human action, is viewed as being within the realm of organized complexity (Klir, 1991, p. 119). Table 1 resumes the relationship between Weaver’s notions of complexity and the suitability of stochastic methods in terms of the respective status of probabilistic statements. It paves the way for bringing risk and its non-probabilistic form (deep uncertainty) as well as complexity, the latter as an answer to research gap II, together in one single scheme.
Table 2: A suggested taxonomy of uncertainties and complexities based on Weaver (1948).
Image

7. CONCLUSION
To conclude this paper, the following Figure 2 integrates the new dimensions around deep uncertainty and scales of measurement in the existing Weaverian framework about the disassembly of the complexity notion and in Mises’s reasoning about the two different types of probability constituting a subclass of deep uncertainty and Risk II, respectively.
Figure 2: The disassembly of complexity: The unifying framework.
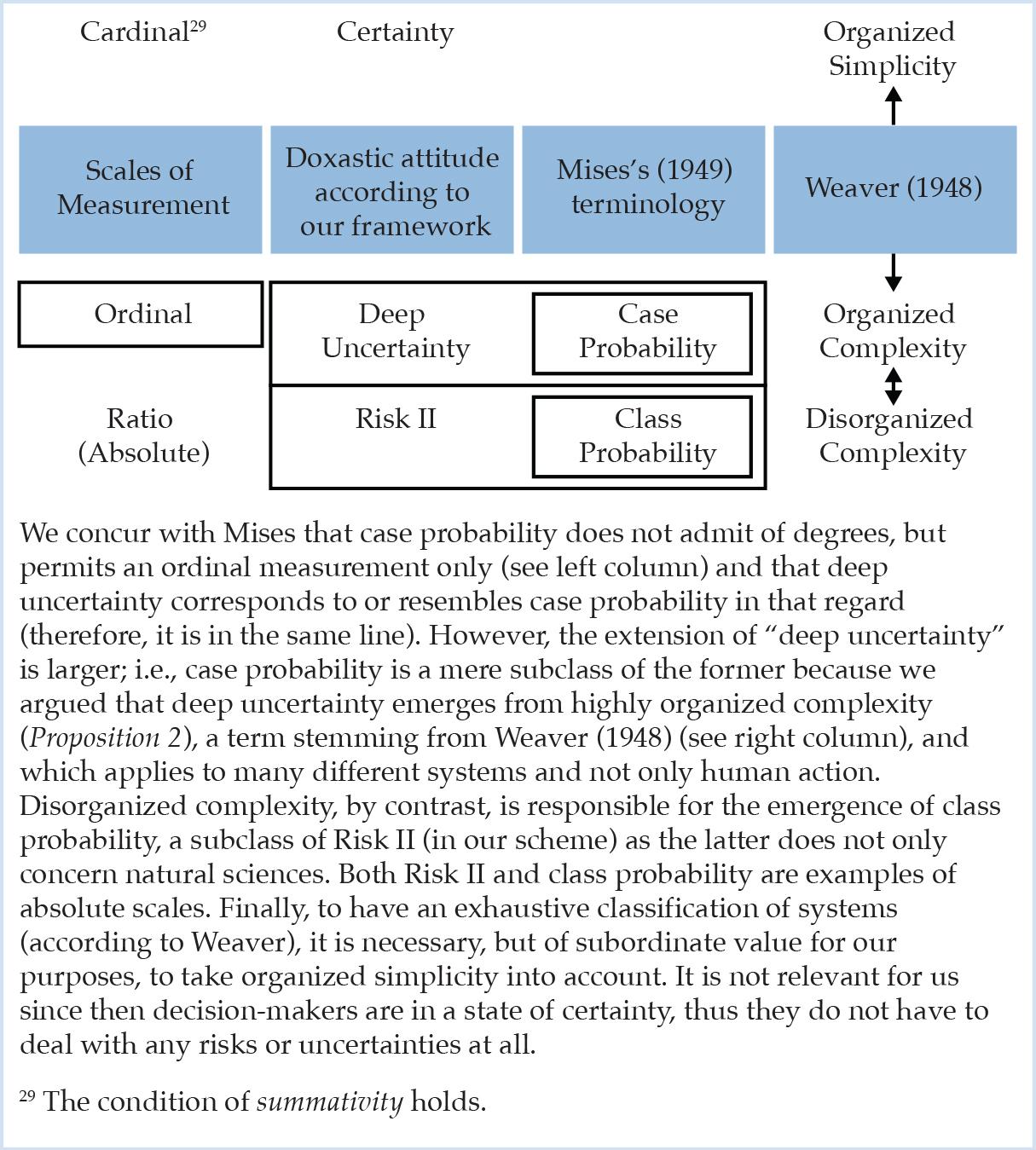
We share the same ground with Mises (1949) and Knight (1921) when we are very wary about the predominance of probability statistics in the realm of economics and finance which is more characterized by case probability, that we presented as a merely comparative notion (Proposition 1), than by class probability. However, many outcomes of this study are not in accordance with the praxeological approach. In light of the two research gaps we singled out, we would like to highlight two instances:
- “Risk” should be grasped as Risk I, not Risk II.
- Not human vs. non-human action (or, phrased positively, human action vs. natural sciences, cf. Mises 1949: 107) decides on the applicability of probability theory, but a system’s degree of organized complexity where deep uncertainty arises from (Proposition 2).
If this study stimulates further controversy of how to conceive risk and identify the limitations of probability theory, as such debate is considered very important for the development of the risk fields (Aven, 2012, p. 34), it will already have served a useful purpose.
- 1The origin of the concept of risk is not clear. Etymologically, the term is, among other things, derived from the Greek word “rhiza” which can be translated with “cliff”, supporting the above negative mode of explanation, and from the Latin vulgar expression “risicare” / “resecare”, meaning “to run into danger” or “to wage / to hazard”. Cf. Heinemann, 2014, p. 59.a
- 1Ellsberg (1961) speaks of the ambiguity of a piece of information.
- 2“Although expectation values have been calculated since the 17th century, the use of the term ‘risk’ in this sense is relatively new. It was introduced into risk analysis in the influential Reactor Safety Study, WASH-1400, (Rasmussen, 1975).” (Hansson, 2011). Today, Hansson (2011) regards it as the standard technical meaning of the term “risk” in many disciplines. Some risk analysts even think that it is the only correct usage of the term (ibid.).
- 3“Most presentations of decision theory work from Luce and Raiffa’s (1957) [building on Knight, 1921; C.H.] classic distinction between situations of certainty (when the consequences of actions are known), risk (when the probability of each possible consequence of an action is known, but not which will be the actual one) and uncertainty (when these probabilities are unknown)” (Bradley and Drechsler, 2014, p. 1229).
- 4x: yes, o: no, x?: answer depending on the meaning of the terms or it is not specified. A similar, but not fully satisfactory summary is found in Aven (2012, p. 37).
- 5However, cf. also Rothbard (1962, pp. 498–501).
- 6A precise definition includes the logical operator “if, and only if”, which is missing in how Mises introduces “probability.”
- 7Moreover, that Mises (1949) shows himself in complete agreement with his brother (Mises, 1939) in this regard, entails that he deliberately uses “random” to mean “chancy,” which is problematic (cf. Eagle, 2012).
- 8The unknown might, therefore, also be knowable insofar as there (will) exist mechanisms that allow transforming the unknown into the known. These mechanisms can be either known or unknown. It is often unknown whether a risk or circumstance is a “knowable unknown” or an “unknowable unknown”, which might remind the reader of Donald Rumsfeld’s dictum of known and unknown unknowns—another demarcation line.
- 10In principle, even higher orders of uncertainty are conceivable.
- 11Following Rothschild and Stiglitz (1970, pp. 226f.), it is, of course, impossible to prove that one definition is better than another. Instead, they point out that definitions are chosen for their usefulness as well as their consistency.
- 12An impressive example of how knowledge is interwoven with our measurement tools can be taken from fractal geometry: Intuitively, we would assume that a question like “How long is the coast of Britain?” is well-defined and can be answered clearly and precisely by pointing to a certain fact. However, by adding to the observations by Lewis Richardson (1881–1953), Mandelbrot (1967) shows that the length of a coastline, a self-similar curve or fractal object, depends on the scale at which it is measured (which has become known as the ‘coastline paradox’).
- 13For example, Mises (1949, p. 874) places the learning of economics within the context of systems thinking and the “interconnectedness of all phenomena of action” at the core of systems thinking.
- 14According to Aven (2012), this premise is not in line with cultural theory and constructivism (cf. also Jasanoff, 1999; Wynne, 1992; and critical comments in Rosa, 1998). Beck (1992, p. 55), for example, writes that “because risks are risks in knowledge, perceptions of risks and risk are not different things, but one and the same.”
- 15Power, for example, to the extent that what counts as a risk to someone may be an act of God to someone else, resigned to his fate (Bernstein, 1996b).
- 16Taleb and Pilpel (2004) and Aven (2012), for example, argue that we should leave the Knightian nomenclature once and for all: “[…] the distinction is irrelevant, actually misleading, since, outside of laboratory experiments, the operator does not know beforehand if he is in a situation of ‘Knightian risk’” (Taleb and Pilpel, 2004, p. 4).
- 17However, the agent’s acting as if the representation is true of her does not make it true of her. Cf. Hájek, 2009, p. 238.
- 18These first two passages are taken from Steigleder (2012, p. 4).
- 19We follow Steigleder (2012, p. 4) in calling an event expectable here “if it is known to be a normal and common consequence of certain circumstances or actions. Whenever an event that is expectable in this sense does not occur, that is something abnormal and needs explanation.”
- 20The need for a response to this challenge also became very clear in the wake of the LTCM case in 1998 (McNeil et al., 2005, p. 20). John Meriwether, the founder of the hedge fund, clearly learned from this experience of extreme financial turbulence; he is quoted as saying: “With globalization increasing, you’ll see more crises. Our whole focus is on extremes now—what’s the worst that can happen to you in any situation—because we never want to go through that again.” (Wall Street Journal, 2000).
- 21The probability of occurrence or at least the subjective probability must be less than 1 and more than 0, otherwise there would be certainty about the event or the possible outcomes of an action. (Going back to Lewis [1980], the principle that, roughly, one’s prior subjective probabilities conditional on the objective chances should equal the objective chances is called the principal principle.) Moreover, the probability should be seen in relation to a fixed and well-defined period of time. For the concept of probability including objective and subjective probabilities, in general, cf. Hájek (2011).
- 22For readers well versed in economic theories of decision sciences, it should be added that, depending on the particular theory, probabilities are not always assigned to the consequences of action alternatives (e.g., Jeffrey, 1983), but also, for example and actually more often, to so-called states of the world (e.g., Savage, 1954).
- 23The risk formula “Risk = probability * measure of severity (e.g., utility, monetary unit, etc.)” directly follows from the Risk II concept (Hansson’s fourth definition). Since Risk II presupposes known probabilities (with 0 < p < 1), decisions under “risk” are made, and not decisions under conditions of “uncertainty” (Hansson’s fifth definition). And, finally, seeing risk as probability (third definition) can be considered a special case of Risk II
- 24A similar illustration (but insufficient explanation of the concepts) is found in Heinemann (2014, p. 61).
- 25See above: “Hence, it is third in turn important to have a risk concept based on probability models to be able to participate in, and contribute to, the discourse of risk if a great number of participants and economists or people interested in risk management in banking, in particular, should be reached. Since such a definition of risk (which will be baptized Risk II) would not do justice to the requirements set above (e.g., the first condition), however, it will not be the one which is pursued and embraced in this study after all.”
- 26We differentiate among four types of scales: nominal, ordinal, interval and ratio. According to Tal (2015, 3.2), “[n]ominal scales represent objects as belonging to classes that have no particular order, e.g., male and female. Ordinal scales represent order but no further algebraic structure” and admit of any transformation function as long as it is monotonic and increasing. Celsius is an example of interval scales: “they represent equality or inequality among intervals of temperature, but not ratios of temperature, because their zero points are arbitrary. The Kelvin scale, by contrast, is a ratio scale, as are the familiar scales representing mass in kilograms, length in meters and duration in seconds.” This classification was further refined to distinguish between linear and logarithmic interval scales and between ratio scales with and without a natural unit (Tal, 2015, 3.2.). “Ratio scales with a natural unit, such as those used for counting discrete objects and for representing probabilities, were named ‘absolute’ scales” (Tal, 2015, 3.2.).
- 27It is an open issue whether the representation of magnitudes on ordinal scales should count as measurement at all (Tal, 2015).


