[Full Issue of the Quarterly Journal of Austrian Economics 20, no. 4 (2017)]
ABSTRACT: Roger Garrison (2001) employs the concept of “secular growth” in which a one-shot (but permanent) fall in time preferences can yield a long string of doses of net investment, so long as gross saving exceeds depreciation. However, Salerno (2001) argues that secular growth is incompatible with orthodox Austrian capital theory, and suggests ways that Garrison’s appeal to neoclassical readers can be maintained while respecting the framework bequeathed by Rothbard. Commenting on the dispute, Young (2009) argues—perhaps ironically—that the mainstream growth literature, steeped in the famous Solow model, comes down on the side of Salerno. The present paper clarifies some ambiguities in Young’s discussion, and then argues that Garrison’s usage of “secular growth” is more likely to resonate with a neoclassical reader than Salerno’s approach. To be sure, Rothbardians may ultimately reject Garrison’s standard exposition (because of Salerno’s objections), but Time and Money still represents a smooth gateway to introduce neoclassical readers to capital-based macroeconomics
KEYWORDS: Solow growth model, secular growth, capital theory
JEL CLASSIFICATION: B25, E21, E22, O11, O12, O16, O43
I. INTRODUCTION
Roger Garrison’s (2001) Time and Money, and its accompanying PowerPoint presentations,1 provide a creative graphical exposition of Austrian macroeconomics in the form of three interlocking diagrams. Specifically, Garrison relates the Hayekian triangle to the “Production Possibilities Frontier” (PPF) so familiar in mainstream textbooks, which in turn he links to a standard loanable funds diagram familiar to Austrians and neoclassicals alike. Besides making for an entertaining seminar presentation, Garrison’s framework thus tells the Mises-Hayek business cycle story in a way that neoclassical economists can understand.2
Although he appreciates Garrison’s return to the fundamentals of Austrian capital, interest, and business cycle theory—what Garrison himself dubs “capital-based macroeconomics”—Joseph Salerno (2001) worries that Garrison has unwittingly employed an analytical concept that conflicts with the verbal-logical foundations of Austrian macroeconomics. Specifically, Garrison adopts a baseline of “secular growth” as more realistic than a stationary (no growth) economy. As Garrison defines the term:
Secular growth occurs without having been provoked by policy or by technological advance or by a change in intertemporal preferences. Rather, the ongoing gross investment is sufficient for both capital maintenance and capital accumulation. (Garrison, 2001, p. 54)
Salerno (2001) argues that this concept of secular growth is dubious from an Austrian perspective. For one thing, Garrison’s discussion suggests that during periods of secular growth the economy is on “autopilot” (my term), whereas the Mengerian tradition roots Austrian analysis as causal from the foundations of the School.3
More specifically, Salerno reminds us that in Rothbard’s treatment (which he viewed as merely elaborating capital theory in the tradition of Böhm-Bawerk, Mises, and Hayek), a change in time preferences corresponds to a new resting state. There may be a transition period as the production structure evolves, but in the Austrian framework
[t]he increase in real income resulting from a given dose of net investment does not buy, as it were, an automatic and continuous flow of extra capital goods that can be utilized for further extensions of the structure of production; all capital goods created by an act of net saving are fully absorbed in maintaining the enhanced flow of real income characterizing the new stationary economy. (Salerno, 2001, p. 45)
Salerno then illustrates his position with a numerical Robinson Crusoe example, in which each period Crusoe engages in discrete acts of net saving, jumping from one stationary economy to the next, in a succession of growing output. Although superficially this may seem like Garrison’s “secular growth,” Salerno argues that it is quite distinct, because each jump involves a further drop in time preference and a conscious decision to accumulate additional capital goods.
I agree with Salerno that Garrison’s notion of “secular growth” is at odds with Rothbard’s treatment in Man, Economy, and State (2004 [1962]). There, a one-shot (and permanent) fall in the community’s time preferences results in a new stationary state for the economy, with a lower interest rate, deeper capital structure, and higher gross investment to maintain it.4 But in Rothbard’s approach, once the economy adjusts to the new parameters, the process stops; we are back in a long-term equilibrium unless something disturbs it. In particular, there is no reason for the capital stock to continue growing, or for the flow of consumer goods to continue rising.
However, in the present paper we are not asking whether Garrison or Salerno has the approach to capital accumulation that is more compatible with Rothbard. Rather, here we focus attention on the narrow question of, “What approach is more likely to resonate with the way neoclassical economists think about capital accumulation?” At first blush, it would seem that Garrison comes out the clear winner, largely because of the way mainstream economists define their terms. In Section II of this paper, we will spell out this affinity between mainstream economics and Garrison’s terminology.
Yet even though I believe it will be easy to demonstrate that mainstream economists would quickly identify with Garrison’s treatment of secular growth, ironically Young (2009) reaches the opposite conclusion. Specifically, Young (2009) argues that neoclassical readers, familiar with the growth literature based on the famous Solow model, would agree with Salerno’s take on the concept of secular growth. In Section III of this paper, I will show that although superficially plausible, Young’s argument falls apart when we consider the time involved in moving to a new “steady state” in the Solow model. Notwithstanding the well-known results of the Solow model concerning savings rates and economic growth, it is still the case that mainstream economists would side with Garrison’s definition of “secular growth” over Salerno’s approach.
II. THE TERMINOLOGY OF MAINSTREAM GROWTH ACCOUNTING
In abstract mathematical models of the economy—such as the canonical Solow growth model—it is customary to treat savings and investment the way that Garrison does in his book. In particular, if we start at a steady-state of no growth, where gross savings each period just balances physical depreciation, and then we suddenly increase the savings rate, there will be a succession of periods of what mainstream economists would label “net investment,” defined as that portion of gross investment that exceeds depreciation.5 (We will go over specific numerical examples of this phenomenon in Section III.)
The mainstream approach lines up perfectly with Garrison’s notion of secular growth in which “the ongoing gross investment is sufficient for both capital maintenance and capital accumulation” (Garrison, 2001, p. 54). In other words, during a period of secular growth, gross investment is high enough that it contains a component covering both depreciation (“capital maintenance”) and a remainder for net investment (“capital accumulation”).
To reiterate, this is how mainstream economists use these terms. To be sure, this labeling would not be due to deep philosophical considerations, but would instead be a matter of definition, carried over from a straightforward accounting treatment in the business world. For example, consider this discussion drawn from Investopedia.com’s entry on “Net Investment”:
If gross investment is consistently higher than depreciation, net investment will be positive, indicating that productive capacity is increasing. Conversely, if gross investment is consistently lower than depreciation, net investment will be negative, indicating that productive capacity is decreasing, which can be a potential problem down the road.6
Thus we see that as a simple matter of definitions, mainstream economists would immediately understand what Garrison means when he describes secular growth occurring when gross investment exceeds depreciation, leading to net investment. In particular, if intertemporal preferences should suddenly change and disrupt an original “steady state” equilibrium, mainstream economists would endorse Garrison’s framework in which there would be many succeeding periods of positive net investment, while the growing capital stock (and hence growing depreciation each period) had not yet caught up with the sudden jump in gross saving/gross investment.
In contrast, I do not think the standard mainstream economist—used to thinking about capital as an aggregate quantity “K”—would be able to make much sense of Salerno’s discussion. Salerno’s point is that an Austrian theorist must view capital as a collection of specific capital goods with specific ends to serve, and in that framework, there are difficulties with Garrison’s approach. Yet these types of worries are not ones that would bother a mainstream economist. He or she would immediately adopt Garrison’s approach to savings rates, gross vs. net investment, and hence secular growth.
III. ANDREW YOUNG PITS SOLOW AGAINST GARRISON
In the previous section, I argued that simply by a matter of definition—and because they think of capital in aggregates like “K” rather than as concrete capital goods embedded in a subjective plan—mainstream economists would more easily embrace Garrison’s approach to “secular growth” than Salerno’s framework. However, there is one glaring complication to my argument: it is well-known in the growth literature that a higher savings rate cannot explain permanent differences in growth rates between countries, at least if we use standard models such as the Solow model.
Aware of this fact, Young (2009) weighs in on the Garrison/Salerno dispute over secular growth, and explains why he thinks neoclassical economists would declare Salerno the victor:
Salerno argues that, in the absence of technological or institutional change, time preferences must be falling over time for capital accumulation to be sustainable. Furthermore, Salerno’s argument echoes one of the primary conclusions of neoclassical growth theory [references omitted]…. As Robert Lucas (2002, p. 29) summarizes: the theory “emphasizes a distinction between ‘growth effects’…and ‘level effects.’…[C]hanges in savings rates are level effects….” In the absence of technological change, only a continually rising savings rate (and falling rate of time preference) can result in secular growth.
[…]
Either Salerno’s argument or that of neoclassical growth theory poses a challenge to Garrison’s theory of secular growth. Furthermore, despite their differences, there is little, if anything, contradictory between the two arguments. Most Austrians are not uncomfortable with diminishing returns, and neoclassical growth theorists would not likely deny that more capitalistic methods of production are also more time-consuming. (Young 2009, pp. 36–37, italics in Young’s original, bold added.)
Although Young’s general summary of the neoclassical growth literature is correct, there are some slight nuances in his handling of the matter that—in this case—actually defeat the purpose of his argument. To demonstrate this, I will first present two numerical counterexamples, and then I will explain in broad terms why Young is wrong to pit the Solow model against Garrison.
Counterexample #1 to Young: Perpetual Growth Despite Diminishing Returns and Constant Savings Rate
The standard Solow growth model—which we will exposit in discrete time—relates output to the input of homogenous capital and homogenous labor:
Yt = F(Kt, Lt)
Every period, output is divided between consumption and investment. Furthermore, capital grows with investment but every period depreciates at some rate δ, where 0 ≤ δ < 1. These considerations give the equations:
Yt = Ct + It
Kt+1 = Kt + It – δKt
One of the defining features of the Solow model (which is relaxed in later models in the neoclassical growth literature) is that the savings rate s, where 0 < s < 1, is exogenous and constant (at least for purposes of determining the “steady state” equilibrium). This gives us:
It = sYt
Kt+1 = Kt + sYt – δKt
Kt+1 = Kt + sF(Kt, Lt) – δKt
In standard expositions of the Solow model, there are more assumptions on the growth of the population, and of a technology parameter that “augments” the labor stock. For our purposes, we can dispense with these complexities, and hold technology and population constant. For simplicity, we will set the labor supply to 1 for all periods.
In this first counterexample, we will set δ=0, meaning that there is no physical depreciation in the capital stock. Further, we set Yt = F(Kt, Lt) = (Kt)1/2(Lt)1/2 = (Kt)1/2. That is, output every period is equal to the square root of the size of the capital stock that period.7 Notice that our production function is an example of the Cobb-Douglas class, with the shares of capital and labor each set to ½.
With this setup, in Table 1 we simulate the evolution of an economy where the initial capital stock is 100.
Table 1: Counterexample #1: An economy with diminishing returns and constant savings rate, yet perpetual growth

In Table 1, we see that the simulated economy enjoys perpetual (and constant) growth, as measured in absolute terms. Specifically, total real output grows by 0.05 units every period. Every period, the additional volume of output is split 10/90 between investment and consumption: Specifically (and as shown in the last column), net investment itself grows by 0.005 units each period, whereas consumption grows by 0.045 units (though space constraints prevent us from showing this in the table). Be careful not to become confused with rates of change: investment (like consumption) is a flow variable that, in this numerical example, itself increases linearly over time. However, the total amount of capital in each period is a stock variable that, in this example, grows exponentially over time.
Note that in this specific numerical example, there is no steady-state to which the economy moves; real output is 0.05 units higher every period, forever. Each period, the community enjoys 0.045 units of more (real) consumption, forever. Furthermore, this perpetual growth occurs despite the fact that we assumed a constant savings rate, and furthermore chose a production function (of the standard Cobb-Douglas class) that exhibits diminishing returns. That is to say, it is still true in this example that a given increase in K leads to ever smaller increases in Y (and hence investment and consumption) as K grows larger. (Thus, if this hypothetical economy experienced a perpetual stream of net investment of the same absolute size every period, then in the long run, the increase in real output each period would tend towards zero.) Nonetheless, there is no tendency in this economy for the growth in real output to asymptotically approach zero, even though there is a constant savings rate and a typical production function. On the contrary, real output grows without limit. Rereading Young’s block quotation above, and contrasting his description with our specific example, it is clear that something is amiss.
The “trick” we’ve used in Counterexample #1—and which is driving the results that probably strike most readers as initially counterintuitive—is that even though the derivative8 of the production function with respect to K is diminishing as K increases, that feature does not imply that output is diminishing with respect to t. As the “Net Investment” column indicates, the periodic increments in K themselves constantly increase over time. Therefore, even though a given dose of additional capital will yield ever diminishing increments in output, perpetually increasing doses of additional capital can yield a constant increment in output over time.9 Indeed, that is exactly what we have illustrated in Table 1.
To be sure, the model depicted in Counterexample #1 is not very realistic. (In the next section we address this concern.) Yet it served the purpose of isolating the role that different assumptions play in yielding the standard results of the Solow model. In particular, Counterexample #1 showed that a constant savings rate plus “diminishing returns in the production function” do not rule out perpetual growth in real output, even though one might have thought otherwise from reading Young’s discussion of the neoclassical growth literature. It should go without saying that Young is aware of the importance of depreciation in these models, but nonetheless the results in Table 1 may be counterintuitive for many readers, and it is important to show that “diminishing returns” by itself does not prevent perpetual growth.
Counterexample #2 to Young: Long-Term (Secular?) Growth Even with Depreciation
An obvious objection to our first counterexample is that it did not include physical depreciation of the capital stock, and thus may have been an unfair test of Young’s position.10 I have two responses to such an objection.
First, even if it were true that employing a positive depreciation rate “fixed” everything and made secular growth once again appear untenable, my first counterexample would still underscore that Young’s emphasis on diminishing returns was not the full story. Young did not mention depreciation in his attempt to unite Salerno with the neoclassicals, and thus Counterexample #1 would be useful if only to clarify the terms of the marriage.
Second and more important, even when we add a positive depreciation rate to the Solow model, it still can take many periods—what we might interpret as “a long time”—for the periodic increases in real output to peter out. We illustrate this possibility in Table 2 where we have made the depreciation rate 5 percent of the existing capital stock, and where we have changed the initial capital stock to 1.000 to make the first few calculations intuitive.
Table 2: Counterexample #2: An economy with diminishing returns, constant savings rate, and depreciation, yet long-lasting growth
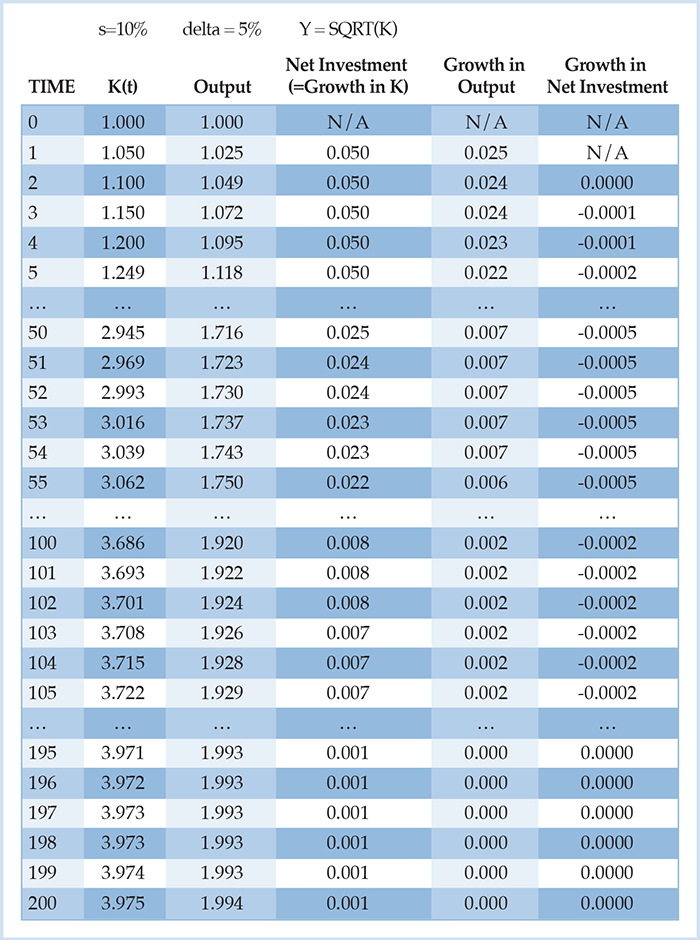
With our chosen parameter values, the typical neoclassical economist would characterize the “steady state” equilibrium by noting that when Kt = 4, investment exactly counterbalances depreciation.11 If the capital stock were ever to exceed the level of 4, then depreciation would exceed gross investment and the capital stock would decline. Thus, once we add in physical depreciation, a constant savings rate—coupled with diminishing returns to capital in the production function—means that real output will indeed approach a plateau. In this case, real output will settle down in the steady state at a level of SQRT(4) = 2.
However, does this mean that Young is right after all, and that a typical neoclassical growth model leaves no room for secular growth in the Garrisonian sense? I would argue no. As Table 2 shows, even though real output is bounded above, it can grow by significant amounts for extended periods.
For example, we can imagine that Table 2 shows the evolution of an economy that starts with an initial savings rate of 5 percent, and then suddenly doubles the savings rate to 10 percent. Note that the time 0 values would constitute an original steady state at the lower savings rate (or higher time preference rate). Specifically, at time 0, if the savings rate is 5 percent, and the capital stock is 1, then investment just balances depreciation.
Now the rest of the table shows what happens if, for some reason, we disrupt that initial steady state by having time preferences suddenly fall, such that the constant savings rate jumps up to 10 percent. In Garrisonian terms, in the immediate aftermath of this preference change, gross investment is more than sufficient to cover depreciation, so that there is net investment—the capital stock grows. Garrison would label this as a period of secular growth.
Now Salerno (and Young) would presumably argue that no, this is not genuine secular growth, because it merely represents a transition period to the new steady state. In particular, once capital has quadrupled to 4, and real output has doubled to 2, gross investment will once again be adequate only to just offset depreciation. Net investment will have fallen to zero.
That is certainly true, but consider the length of this transition period. For one thing, the economy will never quite attain the new steady state, but will only asymptotically approach it. (Such an asymptotic approach is clearly not how Salerno is thinking about the issues, when he has in mind a transition to a new production structure consisting of particular capital goods.) Yet more significant than this mathematical trivia, is the proportion of the ultimate increase that has yet to be reaped after a significant passage of time. For example, note that by period 55, real output is 1.75 units, which is only seven-eighths of its steady state value. If we interpret time periods to be years, then the “transition period” (to which Salerno and Young wish to deny the label “secular growth”) spans at least two generations.
The Speed of Adjustment in the Neoclassical Growth Literature
Our conclusion from Counterexample #2—namely, that the speed of convergence to a new steady state can take a long time—corresponds with the neoclassical growth literature’s attempts to calibrate their models to real economies. For example, using standard parameter values for population growth, depreciation, capital’s share of income, and so forth, Romer (1996) writes in his graduate macro textbook, in his discussion of the Solow model:
Thus in our example of a 10% increase in the saving rate, output is 0.04(5%) = 0.2% above its previous path after 1 year; is 0.5(5%) = 2.5% above after 18 years; and asymptotically approaches 5% above the previous path. Thus not only is the overall impact of a substantial change in the saving rate modest, but it does not occur very quickly. (Romer, 1996, pp. 22–23)
To paraphrase Romer’s analysis, he is saying that when we plug plausible parameters into the Solow growth model, an increase in the savings rate from, say, 20 percent to 22 percent would eventually boost output by 5 percent relative to the original level. However—and this is crucial for our discussion—after the first 18 years of the sudden jump in savings, output would only have closed half of the gap to its new steady-state level.
For another example showing how neoclassical economists view time in growth models, consider the following commentary on a transition from a capital stock below the “golden rule” (GR) level—which, by definition, maximizes steady-state consumption—up to the GR level:
Note that in the transition to the GR [Golden Rule] point, there will be “initial” effects and “long-run” effects. Say we’re below the GR. As we increase savings, there will be a temporary decrease in consumption, and then a long run increase. Why? Because an increase in savings means less consumption right away…. However, as capital accumulates, output increases, and thus so does consumption. This situation gives us a look into why it’s called the Golden Rule…because we sacrifice consumption now for higher consumption for the people of the future. As Mankiw puts it, the welfare of all generations is given equal weight, so sacrifice by this generation is outweighed by the gains of future generations. (Sanders, 2008, p. 4, emphasis added)
As this commentary (which is taken from study notes on the Solow model) indicates, when neoclassical economists say that a higher savings rate cannot explain economic growth, they may be thinking in terms of generations. The time frame is much much longer than, say, Salerno’s thought experiment of Crusoe building a house over the course of 3,000 hours.
Discussion
To be sure, I am not endorsing the way that typical neoclassical economists deploy the Solow model when interpreting economic statistics. In particular, I have argued elsewhere that Romer (who is merely echoing the rest of the profession) is plunging headlong into the fallacy of the naïve productivity theory of interest that Böhm-Bawerk brilliantly refuted so long ago. (Murphy, 2005)
Instead, my modest point is that when economists such as Robert Lucas (whom Young quoted) say that a constant savings rate can only explain level effects, not growth effects, this observation does not pose a problem for Garrison and his notion of secular growth. As we have seen, the standard Solow model—calibrated with plausible parameter values—predicts that a one-time increase in the savings rate would lead to a permanently higher (but constant) level of output, but that this transition process could take decades before the bulk of the increase had been reaped. During those decades, gross investment would be higher than depreciation, such that the capital stock would grow with each successive burst of “positive net investment” (defined in the standard way that accountants and business owners would use the terms). Is this not entirely compatible with the Garrisonian framework?
Young is certainly correct when he points out that the typical neoclassical growth literature—at least with models that exclude the type of positive externalities from investment that Young believes will solve Garrison’s problem—has no room for growth in the steady state as a result of mere capital accumulation.
However, what the neoclassical economist means by “growth in the steady state” is not exactly the same concept as “secular growth” in Garrison’s framework. Now perhaps Garrison did intend to suggest that an economy could experience rightward shifts in its Production Possibilities Frontier (PPF) indefinitely, as the result of a one-shot increase in the savings rate. That would indeed be inconsistent with the neoclassical literature, and indeed would be hard to reconcile with diminishing returns and (physical) depreciation. However, in his diagrams in Time and Money as well as his PowerPoint presentations, Garrison only shows a few periods of secular growth in response to a fall in time preference, all of which is perfectly consistent with the neoclassical treatment.12
IV. CONCLUSION
Garrison’s definition of “net investment” accords with the way accountants, business people, and neoclassical economists use the term. As such, his related notion of “secular growth” will also resonate with mainstream economists. Salerno is right that Garrisonian secular growth is hard to reconcile with Rothbardian capital theory. However, perhaps the primary virtue of Time and Money is its exposition of capital-based macroeconomics in terminology and graphs that non-Austrian economists can understand. On this criterion, Garrison’s “secular growth” passes with flying colors.
There is an admitted complication that Andrew Young has brought up: a well-known result in the growth literature is that a sudden increase in the savings rate does not lead to permanently higher growth in the Solow model. However, all this means is that Garrison should be clear that his concept of secular growth is not permanent, but rather can last “only” 50 years (with plausible parameter values). This presents no problem for his book’s graphs or his PowerPoint presentations, since they only show a few years of “secular growth” where the PPF shifts outward in response to a one-shot increase in savings. There is nothing in Garrison’s exposition that depends on secular growth lasting literally forever, as opposed to (say) only 50 years.
In other words, Garrison’s treatment is entirely compatible with the neoclassical growth literature so long as he clarifies that his “secular growth” is a long-run but not an infinitely long phenomenon.
[The author thanks Joe Salerno for providing unpublished material, and William Barnett, Walter Block, Adam Martin, and an anonymous referee for feedback on earlier drafts. Alan Murphy helped derive results for the continuous-time version of the Solow model.]
- 1Garrison’s series of PowerPoint presentations are available at https://www.auburn.edu/~garriro/tam.htm.
- 2To be sure, not all Austrians are happy with Garrison’s approach. For example, Barnett and Block (2006) reject the Hayekian triangle outright, while Hülsmann (2001) argues that Garrison’s approach to money “is irreconcilable with the standpoint developed in the writings of Menger, Mises, Rothbard, and others,” and indeed that “Garrison’s macroeconomics is…macroeconomics without money” (p. 34).
- 3Salerno (2010) establishes Menger as the founder of a “causal-realist” tradition which was then elaborated by Mises and Rothbard.
- 4For a numerical illustration of Rothbard’s approach to modeling the economy’s growth in response to a one-shot drop in time preferences, see Murphy (2006) pp. 96–98.
- 5A standard graduate level text is Romer (1996), and its introduction and discussion of the basic Solow model is covered in Chapter 1.
- 6Quotation taken from: http://www.investopedia.com/terms/n/netinvestment.asp, accessed January 11, 2017.
- 7Because we have chosen Lt=1 for all t, labor’s contribution to output falls out of the equation.
- 8Of course the derivative is only defined if we recast the model in continuous, not discrete, terms.
- 9We can switch our Solow model to continuous time to verify analytically that our claims do indeed hold, and are not just a fluke of Excel rounding and (perhaps) an inadequate length of time in the simulation. Specifically, with Y(t) = K(t)1/2, and with dK/dt = (0.1)*Y(t), we can use calculus and substitution to determine that the second derivative of K(t) with respect to t is always +0.005, and that the derivative of Y(t) with respect to t is always +0.05. Thus, the relevant columns in Table 1 are not misleading; they accurately depict the operation of the Solow model with our chosen parameters. Additionally, we can determine that K(t) = [(0.05)t + K(0)1/2]2, which grows without limit as t tends to infinity.
- 10In his comment on Young, Engelhardt (2009) also emphasizes the importance of depreciation in the analysis. Specifically, Engelhardt argues that it is not positive externalities, but rather the assumption of no depreciation, that drives Young’s own model of secular growth.
- 11In this case, total output is SQRT(4) = 2. A savings rate of 10 percent thus implies gross investment of 0.2. But the 5 percent physical depreciation rate on the 4 units of capital implies total depreciation of 0.2, which totally absorbs the gross investment leaving 0 net investment. The capital stock will thus be 4 next period, and the period after, forever.
- 12Even if he did not intend it, Garrison’s descriptions could understandably mislead some readers into thinking that a one-shot change in the savings rate could fuel perpetual growth, even with physical depreciation. For example, in his 2003 PowerPoint presentation on “Sustainable and Unsustainable Growth”—available at https://www.auburn.edu/~garriro/ppsus.ppt—at one point in the demonstration the slide reads: “With gross investment greater than capital depreciation, the economy experiences secular growth. This rate of growth is sustainable.” Strictly speaking, Garrison no doubt means that investments that occur because of a (one-shot) fall in time preferences, wherein gross investment exceeds depreciation, will not lead to a boom-bust cycle. However, his statement is definitely liable to lead some readers to conclude that the economy will continue this (“sustainable”) growth indefinitely, and that indeed this is the baseline of real-world economic growth upon which we add technological innovations. If that is what Garrison was trying to convey, then Young is certainly correct: neoclassical economists would argue that such an analysis ignores the straightforward implications of the standard Solow model. Specifically, if we assume diminishing returns to physical capital, and that depreciation is proportional to the stock of capital, then for fixed technology and a constant savings rate, the economy will eventually reach a “steady state” where gross investment just covers physical depreciation.


