[From Man, Economy, and State.]
The basis on which we have been explaining the purchasing power of money and the changes in and consequences of monetary phenomena has been an analysis of individual action. The behavior of aggregates, such as the aggregate demand for money and aggregate supply, has been constructed out of their individual components. In this way, monetary theory has been integrated into general economics. Monetary theory in American economics, however (apart from the Keynesian system, which we discuss elsewhere), has been presented in entirely different terms—in the quasi-mathematical, holistic equation of exchange, derived especially from Irving Fisher. The prevalence of this fallacious approach makes a detailed critique worthwhile.
The classic exposition of the equation of exchange was in Irving Fisher’s Purchasing Power of Money.1 Fisher describes the chief purpose of his work as that of investigating “the causes determining the purchasing power of money.” Money is a generally acceptable medium of exchange, and purchasing power is rightly defined as the “quantities of other goods which a given quantity of goods will buy.”2 He explains that the lower the prices of goods, the larger will be the quantities that can be bought by a given amount of money, and therefore the greater the purchasing power of money. Vice versa if the prices of goods rise. This is correct; but then comes this flagrant non sequitur: “In short, the purchasing power of money is the reciprocal of the level of prices; so that the study of the purchasing power of money is identical with the study of price levels.”3 From then on, Fisher proceeds to investigate the causes of the “price level”; thus, by a simple “in short,” Fisher has leaped from the real world of an array of individual prices for an innumerable list of concrete goods into the misleading fiction of a “price level,” without discussing the grave difficulties which any such concept must face. The fallacy of the “price level” concept will be treated further below.
The “price level” is allegedly determined by three aggregative factors: the quantity of money in circulation, its “velocity of circulation”—the average number of times during a period that a unit of money is exchanged for goods—and the total volume of goods bought for money. These are related by the famous equation of exchange: MV = PT. This equation of exchange is built up by Fisher in the following way: First, consider an individual exchange transaction—Smith buys 10 pounds of sugar for 7 cents a pound.4 An exchange has been made, Smith giving up 70 cents to Jones, and Jones transferring 10 pounds of sugar to Smith. From this fact Fisher somehow deduces that “10 pounds of sugar have been regarded as equal to 70 cents, and this fact may be expressed thus: 70 cents = 10 pounds multiplied by 7 cents a pound.”5 This off-hand assumption of equality is not self-evident, as Fisher apparently assumes, but a tangle of fallacy and irrelevance. Who has “regarded” the 10 pounds of sugar as equal to the 70 cents? Certainly not Smith, the buyer of the sugar. He bought the sugar precisely because he considered the two quantities as unequal in value; to him the value of the sugar was greater than the value of the 70 cents, and that is why he made the exchange. On the other hand, Jones, the seller of the sugar, made the exchange precisely because the values of the two goods were unequal in the opposite direction, i.e., he valued the 70 cents more than he did the sugar. There is thus never any equality of values on the part of the two participants. The assumption that an exchange presumes some sort of equality has been a delusion of economic theory since Aristotle, and it is surprising that Fisher, an exponent of the subjective theory of value in many respects, fell into the ancient trap. There is certainly no equality of values between two goods exchanged or, as in this case, between the money and the good. Is there an equality in anything else, and can Fisher’s doctrine be salvaged by finding such an equality? Obviously not; there is no equality in weight, length, or any other magnitude. But to Fisher, the equation represents an equality in value between the “money side” and the “goods side”; thus, Fisher states:
[T]he total money paid is equal in value to the total value of the goods bought. The equation thus has a money side and a goods side. The money side is the total money paid….The goods side is made up of the products of quantities of goods exchanged multiplied by respective prices.6
We have seen, however, that even for the individual exchange, and setting aside the holistic problem of “total exchanges,” there is no such “equality” that tells us anything about the facts of economic life. There is no “value-of-money side” equaling a “value-of-goods side.” The equal sign is illegitimate in Fisher’s equation.
How, then, account for the general acceptance of the equal sign and the equation? The answer is that, mathematically, the equation is of course an obvious truism: 70 cents = 10 pounds of sugar × 7 cents per pound of sugar. In other words, 70 cents = 70 cents. But this truism conveys no knowledge of economic fact whatsoever.7 Indeed, it is possible to discover an endless number of such equations, on which esoteric articles and books could be published. Thus:
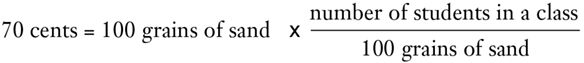
Then, we could say that the “causal factors” determining the quantity of money are: the number of grains of sand, the number of students in the class, and the quantity of money. What we have in Fisher’s equation, in short, is two money sides, each identical with the other. In fact, it is an identity and not an equation. To say that such an equation is not very enlightening is self-evident. All that this equation tells us about economic life is that the total money received in a transaction is equal to the total money given up in a transaction—surely an uninteresting truism.
Let us reconsider the elements of the equation on the basis of the determinants of price, since that is our center of interest. Fisher’s equation of exchange for an individual transaction can be rearranged as follows:
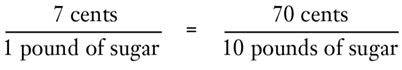
Fisher considers that this equation yields the significant information that the price is determined by the total money spent divided by the total supply of goods sold. Actually, of course, the equation, as an equation, tells us nothing about the determinants of price; thus, we could set up an equally truistic equation:

This equation is just as mathematically true as the other, and, on Fisher’s own mathematical grounds, we could argue cogently that Fisher has “left the important wheat price out of the equation.” We could easily add innumerable equations with an infinite number of complex factors that “determine” price.
The only knowledge we can have of the determinants of price is the knowledge deduced logically from the axioms of praxeology. Mathematics can at best only translate our previous knowledge into relatively unintelligible form; or, usually, it will mislead the reader, as in the present case. The price in the sugar transaction may be made to equal any number of truistic equations; but it is determined by the supply and demand of the participants, and these in turn are governed by the utility of the two goods on the value scales of the participants in exchange. This is the fruitful approach in economic theory, not the sterile mathematical one. If we consider the equation of exchange as revealing the determinants of price, we find that Fisher must be implying that the determinants are the “70 cents” and the “10 pounds of sugar.” But it should be clear that things cannot determine prices. Things, whether pieces of money or pieces of sugar or pieces of anything else, can never act; they cannot set prices or supply and demand schedules. All this can be done only by human action: only individual actors can decide whether or not to buy; only their value scales determine prices. It is this profound mistake that lies at the root of the fallacies of the Fisher equation of exchange: human action is abstracted out of the picture, and things are assumed to be in control of economic life. Thus, either the equation of exchange is a trivial truism—in which case, it is no better than a million other such truistic equations, and has no place in science, which rests on simplicity and economy of methods—or else it is supposed to convey some important truths about economics and the determination of prices. In that case, it makes the profound error of substituting for correct logical analysis of causes based on human action, misleading assumptions based on action by things. At best, the Fisher equation is superfluous and trivial; at worst, it is wrong and misleading, although Fisher himself believed that it conveyed important causal truths.
Thus, Fisher’s equation of exchange is pernicious even for the individual transaction. How much more so when he extends it to the “economy as a whole”! For Fisher, this too was a simple step. “The equation of exchange is simply the sum of the equations involved in all individual exchanges”8 as in a period of time. Let us now, for the sake of argument, assume that there is nothing wrong with Fisher’s individual equations and consider his “summing up” to arrive at the total equation for the economy as a whole. Let us also abstract from the statistical difficulties involved in discovering the magnitudes for any given historical situation. Let us look at several individual transactions of the sort that Fisher tries to build into a total equation of exchange:
- exchanges 70 cents for 10 pounds of sugar
- exchanges 10 dollars for 1 hat
- exchanges 60 cents for 1 pound of butter
- exchanges 500 dollars for 1 television set.
What is the “equation of exchange” for this community of four? Obviously there is no problem in summing up the total amount of money spent: $511.30. But what about the other side of the equation? Of course, if we wish to be meaninglessly truistic, we could simply write $511.30 on the other side of the equation, without any laborious building up at all. But if we merely do this, there is no point to the whole procedure. Furthermore, as Fisher wants to get at the determination of prices, or “the price level,” he cannot rest content at this trivial stage. Yet he continues on the truistic level:

This is what Fisher does, and this is still the same trivial truism that “total money spent equals total money spent.” This triviality is not redeemed by referring to p × Q, p′ × Q′, etc., with each p referring to a price and each Q referring to the quantity of a good, so that: E = Total money spent = pQ + p′ Q′ + p″Q″ + … etc. Writing the equation in this symbolic form does not add to its significance or usefulness.
Fisher, attempting to find the causes of the price level, has to proceed further. We have already seen that even for the individual transaction, the equation p = (E/Q) (price equals total money spent divided by the quantity of goods sold) is only a trivial truism and is erroneous when one tries to use it to analyze the determinants of price. (This is the equation for the price of sugar in Fisherine symbolic form.) How much worse is Fisher’s attempt to arrive at such an equation for the whole community and to use this to discover the determinants of a mythical “price level”! For simplicity’s sake, let us take only the two transactions of A and B, for the sugar and the hat. Total money spent, E, clearly equals $10.70, which, of course, equals total money received, pQ + p′Q′. But Fisher is looking for an equation to explain the price level; therefore he brings in the concept of an “average price level,” P, and a total quantity of goods sold, T, such that E is supposed to equal PT. But the transition from the trivial truism E = pQ + p′Q′ … to the equation E = PT cannot be made as blithely as Fisher believes. Indeed, if we are interested in the explanation of economic life, it cannot be made at all.
For example, for the two transactions (or for the four), what is T? How can 10 pounds of sugar be added to one hat or to one pound of butter, to arrive at T? Obviously, no such addition can be performed, and therefore Fisher’s holistic T, the total physical quantity of all goods exchanged, is a meaningless concept and cannot be used in scientific analysis. If T is a meaningless concept, then P must be also, since the two presumably vary inversely if E remains constant. And what, indeed, of P? Here, we have a whole array of prices, 7 cents a pound, $10 a hat, etc. What is the price level? Clearly, there is no price level here; there are only individual prices of specific goods. But here, error is likely to persist. Cannot prices in some way be “averaged” to give us a working definition of a price level? This is Fisher’s solution. Prices of the various goods are in some way averaged to arrive at P, then P = (E/T), and all that remains is the difficult “statistical” task of arriving at T. However, the concept of an average for prices is a common fallacy. It is easy to demonstrate that prices can never be averaged for different commodities; we shall use a simple average for our example, but the same conclusion applies to any sort of “weighted average” such as is recommended by Fisher or by anyone else.
What is an average? Reflection will show that for several things to be averaged together, they must first be totaled. In order to be thus added together, the things must have some unit in common, and it must be this unit that is added. Only homogeneous units can be added together. Thus, if one object is 10 yards long, a second is 15 yards long, and a third 20 yards long, we may obtain an average length by adding together the number of yards and dividing by three, yielding an average length of 15 yards. Now, money prices are in terms of ratios of units: cents per pound of sugar, cents per hat, cents per pound of butter, etc. Suppose we take the first two prices:
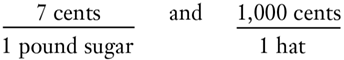
Can these two prices be averaged in any way? Can we add 1,000 and 7 together, get 1,007 cents, and divide by something to get a price level? Obviously not. Simple algebra demonstrates that the only way to add the ratios in terms of cents (certainly there is no other common unit available) is as follows:
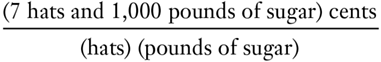
Obviously, neither the numerator nor the denominator makes sense; the units are incommensurable.
Fisher’s more complicated concept of a weighted average, with the prices weighted by the quantities of each good sold, solves the problem of units in the numerator but not in the denominator:
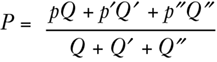
The pQ’s are all money, but the Q’s are still different units. Thus, any concept of average price level involves adding or multiplying quantities of completely different units of goods, such as butter, hats, sugar, etc., and is therefore meaningless and illegitimate. Even pounds of sugar and pounds of butter cannot be added together, because they are two different goods and their valuation is completely different. And if one is tempted to use poundage as the common unit of quantity, what is the pound weight of a concert or a medical or legal service?9
It is evident that PT, in the total equation of exchange, is a completely fallacious concept. While the equation E = pQ for an individual transaction is at least a trivial truism, although not very enlightening, the equation E = PT for the whole society is a false one. Neither P nor T can be defined meaningfully, and this would be necessary for this equation to have any validity. We are left only with E = pQ + p′Q′, etc., which gives us only the useless truism, E = E.10
Since the P concept is completely fallacious, it is obvious that Fisher’s use of the equation to reveal the determinants of prices is also fallacious. He states that if E doubles, and T remains the same, P—the price level—must double. On the holistic level, this is not even a truism; it is false, because neither P nor T can be meaningfully defined. All we can say is that when E doubles, E doubles. For the individual transaction, the equation is at least meaningful; if a man now spends $1.40 on 10 pounds of sugar, it is obvious that the price has doubled from 7 cents to 14 cents a pound. Still, this is only a mathematical truism, telling us nothing of the real causal forces at work. But Fisher never attempted to use this individual equation to explain the determinants of individual prices; he recognized that the logical analysis of supply and demand is far superior here. He used only the holistic equation, which he felt explained the determinants of the price level and was uniquely adapted to such an explanation. Yet the holistic equation is false, and the price level remains pure myth, an indefinable concept.
Let us consider the other side of the equation, E = MV, the average quantity of money in circulation in the period, multiplied by the average velocity of circulation. V is an absurd concept. Even Fisher, in the case of the other magnitudes, recognized the necessity of building up the total from individual exchanges. He was not successful in building up T out of the individual Q’s, P out of the individual p’s, etc., but at least he attempted to do so. But in the case of V, what is the velocity of an individual transaction? Velocity is not an independently defined variable. Fisher, in fact, can derive V only as being equal in every instance and every period to E/M. If I spend in a certain hour $10 for a hat, and I had an average cash balance (or M) for that hour of $200, then, by definition, my V equals 1/20. I had an average quantity of money in my cash balance of $200, each dollar turned over on the average of 1/20 of a time, and consequently I spent $10 in this period. But it is absurd to dignify any quantity with a place in an equation unless it can be defined independently of the other terms in the equation. Fisher compounds the absurdity by setting up M and V as independent determinants of E, which permits him to go to his desired conclusion that if M doubles, and V and T remain constant, P—the price level—will also double. But since V is defined as equal to E/M, what we actually have is: M × (E/M) = PT or simply, E = PT, our original equation. Thus, Fisher’s attempt to arrive at a quantity equation with the price level approximately proportionate to the quantity of money is proved vain by yet another route.
A group of Cambridge economists—Pigou, Robertson, etc.—has attempted to rehabilitate the Fisher equation by eliminating V and substituting the idea that the total supply of money equals the total demand for money. However, their equation is not a particular advance, since they keep the fallacious holistic concepts of P and T, and their k is merely the reciprocal of V, and suffers from the latter’s deficiencies.
In fact, since V is not an independently defined variable, M must be eliminated from the equation as well as V, and the Fisherine (and the Cambridge) equation cannot be used to demonstrate the “quantity theory of money.” And since M and V must disappear, there are an infinite number of other “equations of exchange” that we could, with equal invalidity, uphold as “determinants of the price level.” Thus, the aggregate stock of sugar in the economy may be termed S, and the ratio of E to the total stock of sugar may be called “average sugar turnover,” or U. This new “equation of exchange” would be: SU = PT, and the stock of sugar would suddenly become a major determinant of the price level. Or we could substitute A = number of salesmen in the country, and X = total expenditures per salesman, or “salesmen turnover,” to arrive at a new set of “determinants” in a new equation. And so on.
This example should reveal the fallacy of equations in economic theory. The Fisherine equation has been popular for many years because it has been thought to convey useful economic knowledge. It appears to be demonstrating the plausible (on other grounds) quantity theory of money. Actually, it has only been misleading.
There are other valid criticisms that could be made of Fisher: his use of index numbers, which even at best could only measure a change in a variable, but never define its actual position; his use of an index of T defined in terms of P and of P defined in terms of T; his denial that money is a commodity; the use of mathematical equations in a field where there can be no constants and therefore no quantitative predictions. In particular, even if the equation of exchange were valid in all other respects, it could at best only describe statically the conditions of an average period. It could never describe the path from one static condition to another. Even Fisher admitted this by conceding that a change in M would always affect V, so that the influence of M on P could not be isolated. He contended that after this “transition” period, V would revert to a constant and the effect on P would be proportional. Yet there is no reasoning to support this assertion. At any rate, enough has been shown to warrant expunging the equation of exchange from the economic literature.
- 1Fisher, Purchasing Power of Money, especially pp. 13 ff.
- 2Ibid., p. 13.
- 3Ibid., p. 14.
- 4We are using “dollars” and “cents” here instead of weights of gold for the sake of simplicity and because Fisher himself uses these expressions.
- 5Fisher, Purchasing Power of Money, p. 16.
- 6Ibid., p. 17.
- 7Greidanus justly calls this sort of equation “in all its absurdity the prototype of the equations set up by the equivalubrists,” in the modern mode of the “economics of the bookkeeper, not of the economist.” Greidanus, Value of Money, p. 196.
- 8Fisher, Purchasing Power of Money, p. 16.
- 9For a brilliant critique of the disturbing effects of averaging even when a commensurable unit does exist, see Louis M. Spadaro, “Averages and Aggregates in Economics” in On Freedom and Free Enterprise, pp. 140–60.
- 10See Clark Warburton, “Elementary Algebra and the Equation of Exchange,” American Economic Review, June, 1953, pp. 358–61. Also see Mises, Human Action, p. 396; B.M. Anderson, Jr., The Value of Money (New York: Macmillan & Co., 1926), pp. 154–64; and Greidanus, Value of Money, pp. 59–62.


