Volume 17, No. 3 (Fall 2014)
ABSTRACT: Keynes’s theory of Aggregate Expenditures from the General Theory is examined and criticized. Keynes suggested numerous reasons why his marginal propensity to consume (MPC) might vary across individuals, over different time periods, and might be fundamentally heterogeneous in other respects, but assumed a constant MPC for tractability. He also argued that saving was a leakage (1920, pp. 19–20; 1936, pp. 81–85), but ignored the role of financial intermediation, which makes savings available to finance additional expenditure. More importantly, he ignored the injection of newly-created money which boosts both consumption and investment expenditure but does not depend on saving (Mises, 1949, pp. 567–573). When the amount of saving available to finance consumption and investment expenditure is correctly acknowledged, the effective multiplier is greatly increased, computed now as m = ∆Y/∆AE = 1/(MPS)RRR = 1/((1-MPC)RRR). However, it should be kept in mind that, like the money multiplier, the Keynesian multiplier is merely an upper limit which can only be approached asymptotically and over time. In light of this caveat, the multiplier becomes a relatively unimportant concept. Because the required reserve ratio appears in the corrected multiplier, the significance and potential impact of 100 percent reserve banking reforms are also addressed.
KEYWORDS: Keynesianism, aggregate expenditure, stabilization policy, fiscal stimulus, multiplier effect
JEL CLASSIFICATION: B31, E21, E22, E61, 043
1. INTRODUCTION
Is Keynesian stimulus policy in any sense justifiable or warranted? And has it ever been? Substantial literature argues that it is and has been effective, and will continue to be needed in the future, though it has repeatedly been proven ineffective both empirically and as policy. Nevertheless, it remains the cornerstone of economic policy followed by the U.S. and virtually all advanced economies, and recommended by intergovernmental development lenders, if not actually forced by them on developing nations. This paper will demonstrate that the Keynesian expenditure multiplier is not a positive policy guide, and that Keynesian stabilization policy should be abandoned.
Though not the only economist to advocate counter-cyclical macroeconomic stabilization, Keynes remains strongly identified with all variants of such policy approaches, and they are appropriately characterized as Keynesian (Hansen, 1953; Lerner, 1944; Patinkin, 1963, pp. 343–348; Clarke, 1988; Dimand, 1988; Salant, 1989; and Backhouse, 1995; among many others). Although a distinction can be drawn between theories and policies explicitly proposed by Keynes during his life and in his writings, and those proposed by his many followers (Leijonhufvud, 1968, pp. 6-35), among them Hansen (1932, pp. 305–313 [ch. 20]; 1941, pp. 261–289 [chs. 12 and 13]; 1949, pp. 115–142; 1953, pp. 86–114; 1960, pp. 140–150; 1951, pp. 629–674 [chs. 33–35]; 1964, pp. 11–39, 43–55), Lerner (1936, 1944, pp. 296–312; 1951, pp. 245–258), Meade (1951), Robinson (1953; 1956, pp. 208–221; 1962, pp. 63–69; 1969, pp. 15–39, 91–97), Samuelson (1954), and Salant (1989), the strong common thread of counter-cyclical fiscal activism which Keynesian economics shares with Keynesianism more broadly considered, cannot be denied. Lucas and Sargent (1978) concluded that Keynesian economics had to be abandoned, yet the U.S., like most advanced economies, never really superseded deficit finance except for a brief period in the late 1990s, and returned to it in response to the 2007–2009 recession and its aftermath. Keynesian models never seem to die, notwithstanding clear analytical limitations (Backhouse and Laidler, 2004; De Vroey and Hoover, 2004). The thesis of this paper is that Keynesian stabilization policy is not justified by its purported theoretic foundations in the aggregate expenditures multiplier and the marginal propensity to consume.
The Keynesian Resurgence which started in 2008 is currently scheduled to last until the Second Coming. Perhaps longer. In the eventuality, all but inconceivable to Keynesian-inspired policy-makers and their cheerleaders, that the continued and persistent failure of Keynesian policy leads to it becoming once again widely discredited, new resurgences can be anticipated whenever capitalism fails once and for all, as it had utterly and inexorably during the financial crisis of 2007. This rendered private property obsolete and necessitated a progressive socialism directed by an “elite” of pretentious intellectuals and dirigiste technocrats. Never mind that the elite inspired and presided over the unsustainable expansion which led to the collapse. Predictably, the proposed remedy for failed financial regulation is always expanded, more encompassing, and ideologically triumphalist regulation.
Keynesian policy today is inspired less by serious contemporary economics, whether fallacious or not, than the aspirations of policy makers whose economic impact is aptly described by analogy to navigators who persistently run their ship aground whenever the rising tide threatens to float it free. Some Keynesian proponents acknowledge the recovery attained under the Resurgence has thus far been lackluster, but attribute this to the inadequacy of the stimulus and bailout spending. This in a financial environment where the U.S. has nearly quadrupled the monetary base over a four-year period. Among others, former chair of the Council of Economic Advisors Christine Romer (2011) calls for continued monetary and fiscal stimulus to facilitate continued recovery. She deplores the “theorists” ruled by an arbitrary religious faith that monetary expansion leads to inflation. In her view, policy should be formulated by hard-headed “empiricists” like herself, who can correctly observe that after an unprecedented expansion of base money and increasing money in circulation by over 20 percent since the start of the recession, consumer price index (CPI) inflation has not risen too much above pre-recession levels. In addition to ignoring actual prices actual consumers have actually been paying for actual groceries and gasoline, she also ignores the statistical impact on the CPI of weighting housing costs, which have fallen markedly since the start of the recession, at their higher, pre-recession levels. This makes the CPI understate inflation by overstating the impact of falling rental and real estate markets. Housing prices have fallen the most in the urban markets where they were most overvalued before the speculative bubble burst, which are the only markets captured in the CPI.
Interestingly, Romer’s own empirical research finds that tax cuts are more effective in stimulating the economy than fiscal spending or monetary expansion (Romer and Romer, 2010). The unhelpful and uninformative division of the profession into virtuous and pragmatic “empiricists,” who can formulate effective policy responses, and bad, dogmatic “theorists,” who are mired in non-Keynesian rhetoric, is about as helpful as reviving the division of the profession into “salt-water” and “fresh-water” economists (Krugman, 2009). Salt-water economists were orthodox Keynesians at Eastern Establishment schools and Berkeley. Fresh-water economists were monetarists and New Classicals near the Great Lakes. Where, for example, does the Austrian school fit in these spurious intellectual taxonomies? Keep in mind these are no more than ad hoc rhetorical devices, intended to be abandoned or superseded as convenient. It may be an admirable distinction for the Austrian school to pass under the radar of the economic ideologues, who remain as uniformed about economic reality as they are insistent on asserting their mistaken views in the realm of public policy.
The great moderation, the protracted though clearly unsustainable policy-induced economic expansion of 1982–2007, was a period during which the business cycle was considered as obsolete as Keynesian stabilization policy had previously rendered it during the 1960s. This multiparadigm period was marked by an informal division of labor, with Keynesian and post-Keynesian theorists dominating long-run economic analysis, and new classical economists dominating analysis of short-run phenomena. The Keynesian perspective is that an increase in saving reduces aggregate income in the short run, but somewhat schizophrenically, according to uncontroversial views of long run economic growth typified by the Solow growth model, also contributes to sustainable growth (Welfens, 2011, p. 109).
The remainder of this paper is organized as follows. First, the historical evolution of the theory of the consumption function is developed in section 2, focusing on its implications for the marginal propensities to consume and save. The familiar Keynesian multiplier is derived in section 3. Then, Keynes’s treatment of saving as a leakage is criticized and corrected to account for financial intermediation in section 4. The possibility of accelerated intermediation is discussed in section 5. Implications of 100 percent reserve banking are discussed in section 6, and the impact of hyperbolic time discounting is developed in section 7. Concluding comments are presented as section 8.
2. THEORY
Keynes framed what is now called the absolute income hypothesis defining the traditional or naïve Keynesian consumption function: C = C0 + MPC(Y), whereC0 is autonomous consumption and MPC is the marginal propensity to consume (Keynes 1936, pp. 113–119). Thus consumption expenditure C becomes a function of current income Y. A more sophisticated variant may substitute disposable income Yd which takes into account taxes, transfers, and other sources of income. D’Orlando and Sanfilippo (2010) argued that many results deriving from this naïve model of consumption were both well-grounded on behavioral economics and enjoyed sound empirical support.
Duesenberry (1949) next proposed the relative income hypothesis, arguing that consumption was determined less by current absolute income, but by individuals’ income relative to others in society. He proposed a consumption function in terms of the average propensity to consume C/Y,
Ct/Yt = a – b(Yt/Y0),
where the greater an individual’s consumption Yt exceeded the average Y0, the lower would be their average propensity to consume. Thus, even in very poor and rich societies, the richest will consume less of current income than the poorest, who will consume all or nearly all of their income.
Modigliani and Brumberg (1954) later framed the life-cycle hypothesis, arguing that consumers seek to maximize the intertemporal utility from a stream of consumption expenditure. They demonstrated it was optimal for consumers to smooth consumption even if their income was erratic or varied over the course of their career. This accorded with the observation that typical income patterns tend to rise as a worker gains experience and seniority, peaking just prior to retirement, and then being zero or significantly lower during retirement. Rather than severely restrict consumption early in their careers and during retirement, workers would generally benefit both from borrowing against future expected income to finance higher consumption early in their career, especially if they have high time preference, and later on by saving for retirement.
Modigliani and Brumberg’s life cycle consumption function depended on both accumulated wealth W and current income Y, expressed as
C = aW + bY,
where a is the marginal propensity to consume as a fraction of wealth, and b is the conventional Keynesian MPC. This function can be subsumed into the Keynesian absolute income hypothesis if aW is conflated with Keynes’ C0, autonomous consumption, merely implying the plausible interpretation that C0 rises with higher W. Dividing both sides by current income gives
C/Y = b + a(W/Y),
which gives the relationship between the average propensity to consume (APC, = C/Y) and the ratio of accumulated wealth to current income.
One implication of the life-cycle hypothesis was that worker saving would be determined by the average growth rate of GDP. High growth would reward savers more, and furthermore would encourage additional saving which would be required to enjoy an average standard of living in retirement. Increases in life expectancy or lowering of the retirement age would also encourage greater saving, as workers would have to save for a longer retirement period. Modigliani and Brumberg were able to show that in a steady-state economy, working savers would transfer wealth to retired dissavers as these retired workers used up the wealth they had accumulated earlier. If the population grew over time, there would be relatively more workers and fewer retirees, lowering the burden on the working savers while increasing the benefit to the average retiree, but for a shrinking or aging population, this outcome would be reversed, perhaps unsustainably. Increasing productivity would increase income over time, which would tend to encourage additional saving and increase the stock of wealth, both acting to increase the balance of net saving by workers over dissaving by retirees.
Two problems were raised with the life-cycle hypothesis: 1) empirically, younger workers apparently refrain from borrowing against future expected income in the amount that would maximize their utility given the model’s assumptions; and 2) similarly, it was also observed that retirees generally consume less than is strictly consistent with their actual life expectancy. The failure of younger workers to borrow enough may result from ignoring debt aversion in relatively naïve intertemporal utility functions, and when student debt is considered, today’s young workers do borrow against future expected income, more so than ever before. Today the level of student loan debt for many consumers is comparable to mortgage borrowing. Three explanations were proposed to explain retirees’ failure to consume in accordance with their life expectancy: 1) retirees may overoptimistically estimate their life expectancy; 2) retirees are highly risk averse and cannot easily reenter the workforce except at significantly diminished wages, so they have a precautionary motive to retain substantial savings to cover unforeseen financial contingencies, such as market reversals or medical expenses; and 3) retirees may retain some unconsumed wealth to bequeath to their descendants.
To address perceived shortcomings of earlier consumption theories, Friedman (1957) proposed the permanent income hypothesis. Although his refinement of Modigliani and Brumberg is equivalent to merely extending individual life expectancy to infinity, in terms of interpretation, Friedman distinguished between permanent and temporary income. Extending life expectancy to infinity incorporates a bequest motive. Permanent income includes interest income on accumulated assets, regularly-occurring asset appreciation, and the non-variable component of current income, e.g., that part of attributable to accumulated human capital, as long as worker skills do not become obsolete rapidly. For many salaried workers, the permanent component of their wages is basically the whole amount, as long as workers perceive strong job security. For workers in less secure positions, it would be only the opportunity cost of the next best wage they could receive if they lost their current job. It would not include variable overtime demands or sales commissions, but recurring seasonal variations would average out. Temporary income, the variable component, or income perceived by workers as temporary, does not support much consumption spending—Friedman suggested this component should be saved and only the interest spent on additional current consumption, because then any interest on permanent additions to capital would be an addition to permanent income. It could be argued that low time preference individuals save temporary income to boost their asset stock and therefore increase their permanent income, but that individuals with higher time preference are more prone to spend temporary income immediately.
Both the life-cycle and permanent income hypotheses predict individuals act to smooth consumption over their lifetimes, as that is a utility maximizing strategy in these models. Younger workers with relatively low current incomes should borrow against higher expected future incomes and retirees should dissave (Thaler, 1990, p. 195), though empirically workers either do not typically do this at all, or do so less than the two hypotheses predict (Hall, 1978; Flavin, 1981, 1983; Hall and Mishkin, 1982; Wilcox, 1989; Zeldes, 1989; Singleton, 1990; Campbell and Mankiw, 1990; Carroll, 1994; Shea, 1995; Souleles, 2002; Stephens, 2003). In particular, young workers seem either to pessimistically under-appraise either their own future income stream or overall economy-wide growth, or both (Courant, Granmlich, and Laitner, 1984). Retirees also avoid consuming all remaining wealth as their life expectancy diminishes, perhaps due to bequest motives, or because consuming the whole stock of accumulated assets prior to death would be financially catastrophic, or both. Tests of the permanent income and life cycle hypotheses are highly sensitive to the method for segmenting income and consumption into permanent and transitory components. For example, Shirvani and Wilbratte (2009), using multivariate stochastic detrending, found that permanent consumption is determined by permanent income, but that the transitory component of consumption was not related to either permanent income or transitory income. Zeldes (1989) found that poor household consumption was constrained by current income, but rich household consumption was not.
The persistent failure of any compact single-parameter consumption function to adequately explain real-world consumption behavior led to new efforts to capture additional determinants of consumption behavior. Real-world consumers enjoy consumption, but also desire the security—and perhaps the status—offered by accumulated saving. For example, in his celebrated Diary, Samuel Pepys repeatedly expresses delight in the size of his increasing savings, though perhaps equally so in specific acts of consumption.1 The need for a more realistic and encompassing theory of consumption, combined with the empirical failure of earlier naïve theories, led to a more sophisticated multidimensional approach.
The behavioral life-cycle hypothesis (D’Orlando and Sanfillipo 2010) proposes segregating income and wealth into different categories with different MPCs: current income, savings (current assets), and future income. They note that empirically, consumers demonstrate different responses to changes in different categories of wealth and income, a behavior called mental budgeting. D’Orlando and Sanfillipo credit Keynes with the seminal identification of most of the basic underlying factors explaining consumption behavior: utility maximization based on foresight and calculation, preference for procrastination (high time preference), cognitive scarcity, imitation, status quo bias, short time horizon, prodigality (which may also come from high time preference), mental budgeting (where different accounts are kept for different classes of income, including permanent and transitory, as well as different classes of wealth-bearing assets), risk aversion, ambiguity aversion, and debt aversion.
Consumers characteristically have different MPCs for wealth derived from different sources, from assets which are earning different returns—whether from interest/dividend income or asset appreciation—and for physical assets in different locations, as well as for financial assets with varying degrees of liquidity, or different exposure to various kinds of risk, e.g., foreign-denominated assets exposed to exchange-rate risk, etc. (Thaler, 1994, p. 188). It has also been found that MPCs are magnitude-inconsistent—MPCs for small changes in income and/or wealth are significantly higher than for larger changes (Thaler, 1990; Heath and Soll, 1996; Souleles, 2002).
MPCs also vary with time horizon, that is, they are time-inconsistent in that long-term preferences deviate from the short-term preference for immediate gratification (Rabin, 1998, p. 38), which incidentally explains Pepys’s behavior. Consumers make very patient, low-time-preference tradeoffs between costs and benefits far in the future, but still desire immediate gratification (Ho et al., 2006, p. 21). Behaviorally, consumers also employ imitative or habitual heuristics to avoid the deliberation costs of processing available information or of collecting that information in the first place (Stigler and Becker, 1977, p. 82; Pingle, 2006, pp. 340–342). It has also been suggested that retirees spend less because they can spend more time in leisure activities like food preparation or bargain hunting, and thus their consumption is closer to what the life cycle and permanent income hypotheses predict, though their expenditure is lower (Becker, 1965; Aguiar and Hurst, 2005). Small changes in income are more likely to be perceived and treated as temporary, while sufficiently large changes are likely to be perceived as permanent, resulting in correspondingly large adjustments in consumption spending and living standard. However, this would not explain the behavior of younger workers.
Time preference ensures consumers prefer current to future satisfaction, but their actual behavior suggests an even higher preference for current consumption, such as might be explained by the more distant future appearing less certain, and consumers are increasingly risk averse for decisions which extend over longer time periods (Feldstein, 1985), and are thus exposed to more risk, for a longer period, and of a less definable character. One reason consumers may care less about the future is the uncertainty regarding future consumption opportunities, as well as how their preferences may change between now and then (Thaler et al., 1997, p. 648; Pesteau and Possen, 2006, p. 4). Debt aversion offers an additional reason young workers do not consume more (Thaler, 1992, p. 10), but that may be offset in the data by the massive student loan debt many young workers now accumulate.
One feature of behavioral life cycle models is that consumers do not know if a change in income will be permanent, but to some extent act as if they were, more that the level of uncertainty suggests (Shirvani and Wilbraitte, 2009, p. 59). Consumers behave as if they keep separate mental accounts (Prelec and Lowenstein, 1998), which are subjective rather than precise, and distinguish among current disposable income, with a very high MPC, and current assets, with a much lower or even near-zero MPC (Heath and Soll, 1996, p. 41). Unsurprisingly, future income and assets both have very low MPCs. Welfens (2011, p. 126) suggests high time preference by either consumers or policy makers, perhaps driven by poor institutional arrangements, should influence policy makers to adopt short-run Keynesian policies, because economic growth is not possible unless institutions are changed to favor it.
Seventy years of investigations into Keynesian-inspired consumption theory and a variety of appealingly parsimonious hypotheses have led to the general conclusion that consumer behavior is not so simple after all. And if the MPC cannot be averaged over a whole economy and is not time invariant, there can be no multiplier effect, as the next several sections will demonstrate.
3. DERIVATION OF THE MULTIPLIER
The Keynesian multiplier is derived as follows (Keynes, 1936, ch. 10, pp. 113–131). Y represents income and output, and AE is aggregate expenditures, all measured in dollar terms. Any increase in income and output is decomposed into an infinite stream of increases in expenditure:
∆Y = ∆AE0 + ∆AE1 + ∆AE2 + ∆AE3 + … + ∆AEn + …
Each element in this infinite sum is related to the immediately preceding element by the marginal propensity to consume (MPC). Keynes also defines the marginal propensity to save (MPS). Any change in disposable income is divided between consumption and saving, so the marginal propensities to save and consume add to one: 1 = MPC + MPS. Although the MPC may vary across individuals, in Keynes’s construction there is one overall average MPC for the economy at any point in time, so the MPC is assumed to have a constant value less than 1.00 and usually greater than 0.50:
∆Y = ∆AE0 + (MPC)∆AE0 + (MPC)∆AE1 + (MPC)∆AE2 + … + ∆AEn + …
Because the MPC relates each element in the series to the one preceding, the series can be expressed exclusively in terms of the initial increase in expenditure and progressively higher orders of the MPC:
∆Y = ∆AE0 + (MPC)∆AE0 + (MPC)2∆AE0 + (MPC)3∆AE0 + … + (MPC)n∆AE0 + …
Note, however, that MPC heterogeneity derived from time and magnitude inconsistency breaks down the logic of this derivation in a way that mere aggregation over heterogeneous agents does not. Given the implicit assumption that the aggregate or economy-wide MPC is time invariant over the period it takes to arrive at the final change in income ∆Y, this is equivalent to the infinite convergent series:
∆Y = (MPC)0∆AE0 + (MPC)1∆AE0 + (MPC)2∆AE0 + (MPC)3∆AE0 + … + (MPC)n∆AE0 + …
which can be expressed as:
∆Y = ∑i=0,∞(MPC)n∆AE0 = ∆AE0∑i=0,∞(MPC)n
Finally, for infinite convergent sums, and dividing ∆Y by the initial ∆AE to define the multiplier, we have:
m = ∆Y/∆AE = 1/(1 – MPC) = 1/MPS
It is important that the MPC be strictly less than one for the infinite sum to converge. Although some individuals could conceivably spend more than their whole income through borrowing, transfers, confidence fraud, etc., the economy-wide average cannot exceed one. Even when institutionalized under government sponsorship, confidence fraud does not increase aggregate wealth or income.
For agents with high time preference, the MPC is very high in the short run, but diminishes as additional rounds of consumption occur. For agents with low time preference, the MPC is initially low and remains low for later rounds of expenditure.2 The great sin in Keynes’s view is having too low an MPC, and therefore too high an MPS (Keynes, 1920, p. 20; 1936, pp. 81–85, 116–119). This view ignores the possibility of financial intermediation, not to mention monetary injection.
4. THE MULTIPLIER WITH FINANCIAL INTERMEDIATION
We start as before, with a hypothesized increase in total income and output being arrived at as the infinite sum of a series of increases in expenditure:
∆Y = ∆AE0 + ∆AE1 + ∆AE2 + ∆AE3 + … + ∆AEn + …
Some part of each increment of income received as expenditure, measured by the MPC, is immediately spent on consumption goods. At the outset however, we differ from Keynes by observing that the part not spent on consumption, measured by the MPS, does not simply disappear, as Keynes assumed, but is placed in the hands of financial intermediaries3 who lend a good part of this portion to finance investment expenditures. The amount of each increment of expenditure loaned out by the financial intermediaries to finance investment is given by MPS(1 – (RRR), where RRR is the required reserve ratio.4 RRR is conventionally thought of as being arbitrarily set by regulatory authorities, currently approximately 10 percent for the U.S. In practice, this quantity can be thought of as the actual bank intermediation rate, which captures not only banks’ required reserves, but excess reserves they hold voluntarily hold over and above the amount dictated by the reserve requirement, as well as loan loss reserves on time deposits not subject to the reserve requirement. For expository convenience and simplicity, all deposits are treated the same.
In Keynes’s formulation, each element in the expenditure series was related to the preceding by the MPC, but in adapting Keynes’s multiplier scheme to account for financial intermediation, we can see that each element is related to the preceding by MPC + MPS(1 – RRR). Since MPC + MPS = 1, we can rewrite this constant as 1 – MPS + MPS – MPS(RRR) or 1 – MPS(RRR). Thus, each increment of expenditure is reduced from the preceding one by a far smaller amount:
∆Y = ∆AE0 + (1-MPS(RRR))∆AE0 + (1-MPS(RRR))∆AE1 + (1-MPS(RRR))∆AE2 + … + ∆AEn + …
Following the standard derivation, each increment of expenditure can be expressed in terms of the initial one:
∆Y = ∆AE0 + (1-MPS(RRR))∆AE0 + (1-MPS(RRR))2∆AE0 + (1-MPS(RRR))3∆AE0 + … + (1-MPS(RRR))n∆AE0 + …
And the whole series can be expressed as higher orders of (1-MPS(RRR)):
∆Y = (1-MPS(RRR))0∆AE0 + (1-MPS(RRR))1∆AE0 + (1-MPS(RRR))2∆AE0 + (1-MPS(RRR))3∆AE0 + … + (1-MPS(RRR))n∆AE0 + …
This can be expressed as:
∆Y = ∑i=0,∞(1-MPS(RRR))n∆AE0 = ∆AE0∑i=0,∞(1-MPS(RRR))n
And for infinite convergent sums, we can now write the multiplier as:
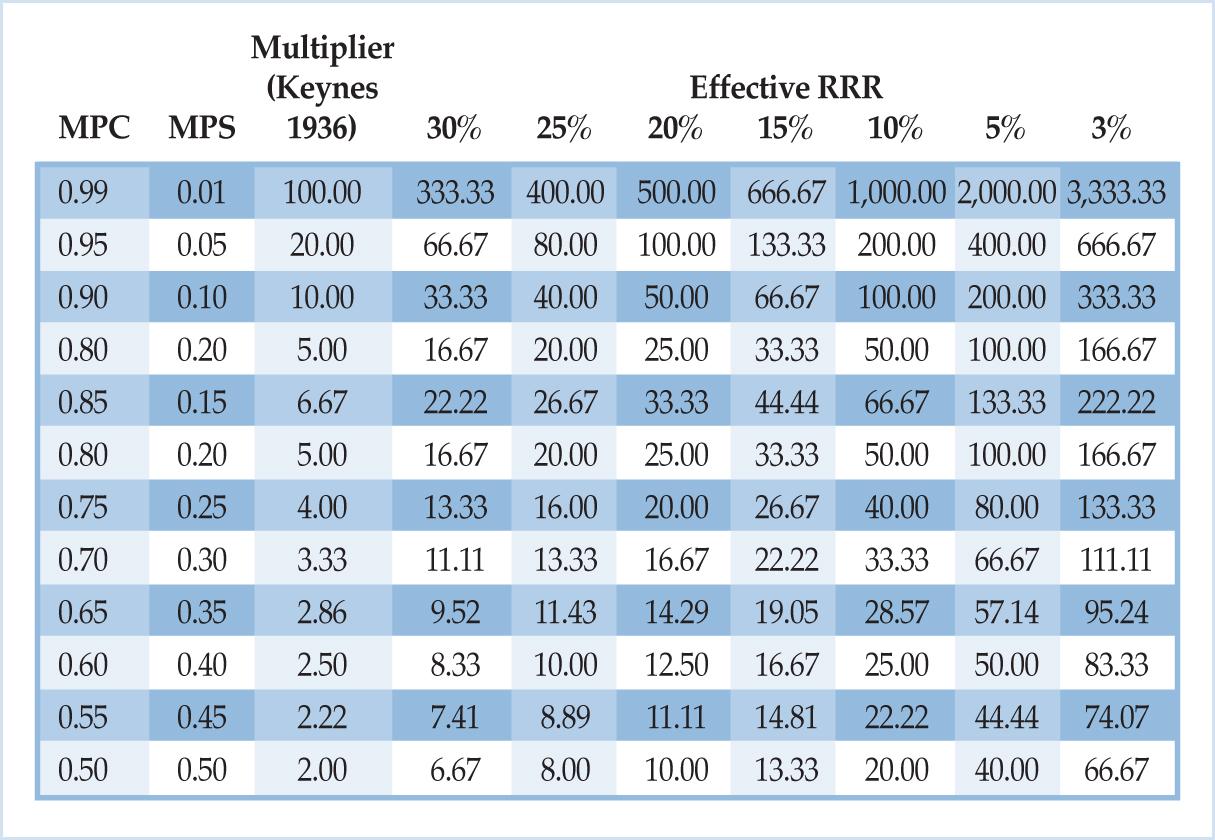
m = ∆Y/∆AE = 1/(MPS(RRR)) = 1/((1-MPC)(RRR))
Table 1. Modified Keynesian Multipliers as a Function of the Effective Reserve Ratio
Note particularly that even with very high reserve requirements, the multipliers adjusted for intermediation are much higher than Keynes suggested. One consequence of this finding is that, far from being a drag on the economy or a leakage out of current expenditure, the amount of income saved boosts the multiplier substantially. If the reserve requirement is ten percent, each dollar saved results in ten times as many dollars of additional income as Keynes suggested, irrespective of how the MPC may vary throughout the economy.
Keynes introduced the now-familiar, though quite obviously wrong, idea that saving represents a drag on output in The Economic Consequences of the Peace (Keynes, 1920, pp. 19–20). In the Treatise on Money (Keynes, 1930 I, p. 279) he attributes recessions to a mistaken tendency for agents to save in excess of investment, rather than for investment to exceed saving. Apparently here he was referring to the economy after a collapse of aggregate expenditure, rather than during the unsustainable expansion which would have to precede a recession. According to the Treatise on Money, too much saving causes recessions (Keynes 1930 I, pp. 172–179), but by the time of the General Theory, saving and investment are always equal by definition (Keynes, 1936, pp. 74–85), though saving remains a necessary evil.5
5. THE AGGREGATE EXPENDITURE MULTIPLIER AND THE MONEY MULTIPLIER
The derivation presented in section 3 above makes the relatively reasonable assumption that each round of additional investment expenditure simultaneously accompanies each additional round of lending by the financial intermediaries. But what if financial intermediation happens significantly faster? Clearly, under appropriate circumstances, banks can lend money more rapidly than borrowers can spend it on consumption, and indeed, until the funds are spent on consumption, they are saved. Except for the small fraction held as bank reserves, these unspent funds are available to be loaned out.
This section presents a derivation of the multiplier with instantaneous, or at least, very rapid, financial intermediation. Now each element in the summation is related to the one preceding not by MPC + MPS(1 – RRR), but by the much greater quantity MPC + MPS(1 – RRR)/RRR. Here the amount of additional income which is spent on consumption is the same as in Keynes’s original multiplier, but now, instead of the remainder being a leakage, the unspent portion is loaned out in successive rounds of lending determined by the money multiplier. Therefore the second term in the constant is multiplied by m = 1/RRR, assuming that deposit expansion occurs instantaneously, or at least, before the next round of additional expenditure. The constant relating different rounds of expenditure can be rewritten as
1 – MPS + MPS/RRR – MPS = 1 – 2MPS + MPS/RRR = 1 – [2MPS – MPS/RRR].
This quantity is greater than one for any values of the MPS, MPC, or any non-zero reserve requirement, and thus the multiplier cannot be derived, because the summation never converges. If we could perform financial intermediation quickly and efficiently enough, income and expenditure could expand without limit. In this situation, the reserve requirement is not adequate by itself to limit the amount of income, even if it can limit the money supply.
6. IMPLICATIONS FOR THE MULTIPLIER UNDER 100 PERCENT RESERVE BANKING
Under 100 percent reserve banking, the reserve requirement becomes 100 percent, so the multiplier would reduce to its familiar Keynesian form given in the General Theory:
m = ∆Y/∆AE = 1/(MPS)RRR = 1/(1-MPC)RRR = 1/(MPS) = 1/(1-MPC)
However, under 100 percent reserve banking, the 100 percent reserve requirement would apply to demand deposits and other deposit instruments commonly available today. It appears highly likely that the financial services industry would respond to the imposition of 100 percent reserve banking by introducing innovative products to facilitate intermediation while rewarding depositors with higher returns. No one has claimed that implementation of 100 percent reserve banking would result in immediate and permanent disintermediation, or that this would be a desirable outcome. If savings go predominantly into instruments for which the 100 percent reserve requirement is inapplicable, the multiplier would be jointly determined by the MPS, the MPC, and the bank intermediation rate or effective reserve ratio, just as described in section 3 above.
7. THE MULTIPLIER WITH HYPERBOLIC DISCOUNTING
Given Keynes’s implicit assumption that the MPC is time invariant, it becomes interesting to see how relaxing this assumption changes the multiplier. Recall the familiar infinite convergent series:
∆Y = (MPC)0∆AE0 + (MPC)1∆AE0 + (MPC)2∆AE0 + (MPC)3∆AE0 + … + (MPC)n∆AE0 + …
This formulation assumes the more familiar exponential discounting. If the MPC diminishes over time, this can be modeled with hyperbolic discounting. Far from being an arbitrary counterfactual, hyperbolic discounting is well established in the behavioral economics literature (Strotz, 1956; Phelps and Pollak, 1967; Laibson, 1997; Angeltos, 2001, p. 50, n. 13; Frederick et al., 2002, p. 360; Ho et al., 2006, p. 21; D’Orlando and Sanfilippo, 2010). The original exponentially-convergent series can be replaced by an expression which diminishes for subsequent rounds of additional expenditure, such as
MPC’ = MPC/(1+n)
This changes the infinite series to
∆Y = (MPC)0∆AE0 + (1/2)(MPC)1∆AE0 + (1/3)(MPC)2∆AE0 + (1/4)(MPC)3∆AE0 + … + (1/1+n)(MPC)n∆AE0 + …
Which can be expressed as:
∆Y = ∑i=0,∞(1/1+n)(MPC)n∆AE0 = ∆AE0∑i=0,∞(MPC)n/(1+n)
Because each item in the summation is smaller than for the Keynesian multiplier, this series converges more rapidly, so unambiguously m’ << m, or in other words:
m’ = ∆Y/∆AE << 1/(1 – MPC) = 1/MPS
An even more extreme, though fortunately more tractable and intuitive approach is to assume future discounting is so extreme that all future consumption is ignored beyond one time period. Then the infinite sum is replaced with:
∆Y = (MPC)0∆AE0 + (MPC)1∆AE0 = ∆AE0(1 + MPC)
The multiplier is then derived as:
m = ∆Y/∆AE = 1 + MPC = 2 – MPS
This preserves the Keynesian conclusion that the higher the MPC and the lower the MPS, the higher the multiplier. The upper bound of two it suggests happens to accord well with empirical findings (Bodkin and Eckstein, 1985, Romer and Romer, 2010), however this has to be taken with a grain of salt. Many empirical estimates of the multiplier are less than one, (e.g., Barro and Redlick, 2010), implying both a negative MPC and an MPS greater than one. The deceptively simple concept of the MPC having a single, constant, time-invariant, time-consistent, and economy-wide value has to be abandoned, and Keynesian stimulus and stabilization policy along with it.
8. CONCLUSION
Keynesian stabilization policy has informed and inspired government responses to the 2007 financial crisis and the 2008–2010 recession. Keynesian economics does not attempt to address the unsustainable expansions which render recessions inevitable. In fact, credit expansion and artificially low interest rates were policy choices pursued aggressively and almost unwaveringly from 1982 to the present. It is difficult for any objective observer to conclude that Keynesian economics offers plausible or especially enlightening explanations for this experience. The Keynesian resurgence is not in any way a resurgence of Keynesian economics, or in any way an intellectual resurgence of ideas that were thoroughly discredited by the stagflation in the 1970s. What we are seeing is merely a resurgence of Keynesian rhetoric in the realm of public policy, trotted out once again to justify a blatantly ineffective and indefensible expansionary policy. Credit expansion got us into this hole, and more credit expansion should not be expected to dig us out.
Sustainable economic growth depends on individual producers’ freedom to divide their income into consumption and saving in accordance with their own preferences, not the preferences assumed for them by politicians and bureaucrats. It is a bizarre delusion to argue that a sustainable outcome which reflects agent preferences can be improved by manipulating interest rates or credit markets. At best, such manipulations can only increase short-term production through inflation. As repeated experience has demonstrated, they can also bring about speculative bubbles and recurrent recessions which make welfare-maximizing consumption smoothing impossible. Monetary expansion and deficit financing should hardly be promoted as welfare-enhancing policy measures, the Keynesian resurgence notwithstanding.
- 1Pepys (1893, vol. 1, pp. 34, 56, 155, 158–159, 194–195, 219, 234, 253, 274, 283, 292, 322; vol. 2, pp. 39, 93, 152, 231, 235, 254, 276, 303, 327, 351, 380, 400, 405; vol. 3, pp. 74, 94, 142, 173, 175, 216, 272, 303, 338, 370; vol. 4, pp. 88, 116, 137, 161, 191, 217, 261, 278, 398, 323, 328, 341, 361, 378, 398; vol. 5, pp. 2, 33, 42, 57, 173, 225, 246, 265, 285, 331, 362; vol. 6, pp. 42, 112, 190). He also expresses significant discomfort the one time his net worth declined (vol. 1, p. 253), but to be quite accurate, his delight in consuming food, wine, entertainment, etc. is just as well documented and equally noteworthy.
- 2This points to the efficacy of hyperbolic, rather than standard exponential, discounting, which has been explored in the behavioral economics literature (Strotz, 1956; Phelps and Pollak, 1967; Laibson, 1997; Angeltos, 2001, p. 50, n. 13; Frederick et al., 2002, p. 360; Ho et al., 2006, p. 21; D’Orlando and Sanfilippo, 2010).
- 3Banks and other financial intermediaries act solely as middlemen when they lend person A’s deposits to person B. In principle, A could lend to B directly, so the bank is nothing more than a middleman in this case. However, most bank intermediation today relies on credit creation by banks—when the bank lends A’s deposits to B, A can still spend their demand deposits or withdraw their time deposits, and now so can B. Here, banks are not purely middlemen, but increase the amount of money in circulation by creating additional credit. Credit created by private banks is sometimes called intermediated credit. Monetary expansion by the central bank encourages credit creation by increasing private bank lending, while making additional funds available for that purpose, increasing the multiplier as described in this section. To distinguish credit created through fractional reserve banking (intermediated credit) from credit which results from an expansionary money supply, the latter is sometimes called injected credit (Cochrane, Call, and Glahe, 1999). The distinction is significant but has no bearing on the present discussion. I am greatly indebted to an anonymous reviewer for pointing out this distinction as a potential source of confusion.
- 4The RRR is formally a regulatory constraint set by the central bank or other authority, but banks typically hold non-zero excess reserves in addition. The actual amount of unloaned deposits banks hold is determined by their effective reserve ratio. Although in reality, this varies with banks’ risk tolerance, awareness of actual risk exposure, and differences in the kinds of lending particular institutions specialize in, etc. these real-world variations can be ignored for the present discussion. The effective reserve ratio for demand deposits is directly analogous to the loan loss reserve ratio held on saving or time deposits. Thus the presentation applies equally well to all deposits.
- 5Robinson (1969, pp. 95–97) makes the more sophisticated observation that saving is necessarily neither good nor bad. Its contribution to economic growth depends on whether it is invested and how productive those investment goods turn out to be. This comes close to approaching the Austrian school’s doctrine of capital multispecificity (Lachmann, 1956, pp. 2–3).

